题目内容
(本小题满分12分)已知 ,且
,且
求证:
 ,且
,且
求证:

见解析。
本试题主要是考查了运用不等式的思想,证明和求解参数x,y,z的取值范围问题。根据已知中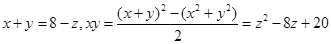 ,然后消去一个未知数,然后利用韦达定理的思想来求解范围。
,然后消去一个未知数,然后利用韦达定理的思想来求解范围。
证明:显然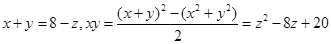
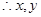 是方程
是方程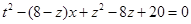 的两个实根,
的两个实根,
由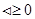 得
得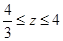 ,同理可得
,同理可得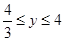 ,
,
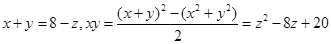 ,然后消去一个未知数,然后利用韦达定理的思想来求解范围。
,然后消去一个未知数,然后利用韦达定理的思想来求解范围。证明:显然
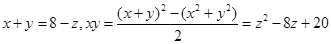
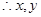 是方程
是方程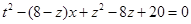 的两个实根,
的两个实根,由
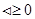 得
得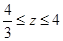 ,同理可得
,同理可得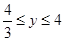 ,
,

练习册系列答案
相关题目
题目内容
 ,且
,且

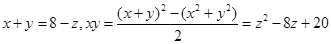 ,然后消去一个未知数,然后利用韦达定理的思想来求解范围。
,然后消去一个未知数,然后利用韦达定理的思想来求解范围。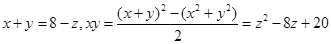
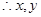 是方程
是方程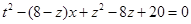 的两个实根,
的两个实根,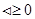 得
得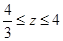 ,同理可得
,同理可得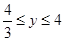 ,
,
