题目内容
【题目】设数列{an}的前n项和为Sn , 且Sn=n2﹣4n﹣5
（1）求数列{an}的通项公式；
（2）设bn=|an|，数列{bn}的前n项和为Tn， 求Tn ．
【答案】（1）
（2）
【解析】
（1）由Sn=n2﹣4n﹣5，可得当n≥2时，an=Sn﹣Sn﹣1=2n﹣5，再检验当n=1时，a1是否适合上式，即可求得数列{an}的通项公式；
（2）由bn=|an|=|2n﹣5|，分n=1、n=2、n≥3三类讨论，分别求得数列{bn}的前n项和Tn，最后综合起来即可求．
（1）解：∵Sn=n2﹣4n﹣5，
∴当n≥2时，an=Sn﹣Sn﹣1=n2﹣4n﹣5﹣[（n﹣1）2﹣4（n﹣1）﹣5]=2n﹣5，
又当n=1时，a1=﹣8不适合上式，
∴
（2）解：∵bn=|an|，数列{bn}的前n项和为Tn，
当n=1时，b1=|a1|=8，T1=8；
当n=2时，b2=|a2|=1，T2=8+1=9；
∵n≥3时，an=2n﹣5≥1＞0，
∴bn=|an|=an=2n﹣5，
∴Tn=8+1+（1+3+…+2n﹣5）=9+ 
=（n﹣2）2+9=n2﹣4n+13．
综上，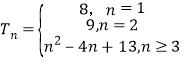 
练习册系列答案
相关题目
【题目】一个车间为了规定工时定额，需要确定加工某种零件所花费的时间，为此进行了6次试验，收集数据如下：
零件数 |
|
|
|
|
|
|
加工时间 |
|
|
|
|
|
|
（Ⅰ）在给定的坐标系中划出散点图，并指出两个变量是正相关还是负相关；
（Ⅱ）求回归直线方程；
（Ⅲ）试预测加工
个零件所花费的时间？
附：对于一组数据
，
，……，
，其回归直线
的斜率和截距的最小二乘估计分别为：
.
