题目内容
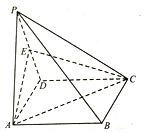
【题目】在平面直角坐标系![]() 中, 圆
中, 圆![]() 为
为![]() 的内切圆.其中
的内切圆.其中![]() .
.
(1)求圆![]() 的方程及
的方程及![]() 点坐标;
点坐标;
(2)在直线 ![]() 上是否存在异于
上是否存在异于![]() 的定点
的定点![]() 使得对圆
使得对圆![]() 上任意一点
上任意一点![]() ,都有
,都有![]() 为常数 )?若存在,求出点
为常数 )?若存在,求出点 ![]() 的坐标及
的坐标及![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() .
.
【解析】
(1)圆![]() 的圆心为
的圆心为![]() ,利用点到直线距离公式,求得半径
,利用点到直线距离公式,求得半径![]() ,得到圆的方程
,得到圆的方程![]() ,再由线段
,再由线段![]() 、线段
、线段![]() 均与圆相切,得到点
均与圆相切,得到点![]() ;
;
(2)假设存在![]() 为常数 ),设
为常数 ),设![]() ,几何关系坐标化,转化成恒成立问题,进而得到
,几何关系坐标化,转化成恒成立问题,进而得到![]() 或
或![]() ,分别代入
,分别代入![]() 并进行检验,得到定点
并进行检验,得到定点![]() .
.
(1)由![]() 知直线
知直线![]() 的方程为
的方程为![]() ,
,
由于圆![]() 与线段
与线段![]() 相切,所以半径
相切,所以半径![]() 即圆
即圆![]() 的方程为
的方程为![]() .
.
由题意![]() 与线段
与线段![]() 相切,所以线段
相切,所以线段![]() 的方程为
的方程为![]() ,即
,即![]() .
.
又![]() 与线段
与线段![]() 也相切,所以线段
也相切,所以线段![]() 的方程为
的方程为![]() ,即
,即![]() .
.
故![]()
(2)设![]() ,则
,则![]() ,
,![]() ,
,
若在直线![]() 上存在异于
上存在异于![]() 的定点
的定点![]() ,使得对圆
,使得对圆![]() 上任意一点
上任意一点![]() ,
,
都有![]() 为常数 ),等价于
为常数 ),等价于![]() ,
,
对圆![]() 上任意点
上任意点![]() 恒成立.
恒成立.
即![]()
整理得:![]()
因为点![]() 在直线
在直线![]() 上,所以
上,所以![]() ,由于
,由于![]() 在圆
在圆![]() 上,所以
上,所以![]() .
.
故![]() 对任意
对任意![]() 恒成立,
恒成立,
所以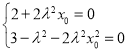 显然
显然![]() ,所以
,所以![]() 故
故![]() ,
,
因为![]() ,解得:
,解得:![]() 或
或![]() ;
;
当![]() 时,
时,![]() 此时
此时![]() 重合,舍去.
重合,舍去.
当![]() 时,
时,![]()
综上,存在满足条件的定点![]() ,此时
,此时![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】已知椭圆![]() :
:![]() 的左、右焦点分别为
的左、右焦点分别为![]() ,
,![]() ,若椭圆经过点
,若椭圆经过点![]() ,且
,且![]() 的面积为
的面积为![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设斜率为![]() 的直线
的直线![]() 与以原点为圆心,半径为
与以原点为圆心,半径为![]() 的圆交于
的圆交于![]() ,
,![]() 两点,与椭圆
两点,与椭圆![]() 交于
交于![]() ,
,![]() 两点,且
两点,且![]() ,当
,当![]() 取得最小值时,求直线
取得最小值时,求直线![]() 的方程.
的方程.
【题目】在十九大“建设美丽中国”的号召下,某省级生态农业示范县大力实施绿色生产方案,对某种农产品的生产方式分别进行了甲、乙两种方案的改良。为了检查甲、乙两种方案的改良效果,随机在这两种方案中各任意抽取了40件产品作为样本逐件称出它们的重量(单位:克),重量值落在![]() 之间的产品为合格品,否则为不合格品。下表是甲、乙两种方案样本频数分布表。
之间的产品为合格品,否则为不合格品。下表是甲、乙两种方案样本频数分布表。
产品重量 | 甲方案频数 | 乙方案频数 |
| 6 | 2 |
| 8 | 12 |
| 14 | 18 |
| 8 | 6 |
| 4 | 2 |
(1)根据上表数据求甲(同组中的重量值用组中点数值代替)方案样本中40件产品的平均数和中位数
(2)由以上统计数据完成下面![]() 列联表,并回答有多大把握认为“产品是否为合格品与改良方案的选择有关”.
列联表,并回答有多大把握认为“产品是否为合格品与改良方案的选择有关”.
甲方案 | 乙方案 | 合计 | |
合格品 | |||
不合格品 | |||
合计 |
参考公式:![]() ,其中
,其中![]() .
.
临界值表:
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.814 | 5.024 | 6.635 | 10.828 |