题目内容
定义在R上的函数f(x)满足:如果对任意x1,x2∈R,都有 ,则称f(x)是R上凹函数.已知二次函数f(x)=ax2+x(a∈R,且a≠0).
,则称f(x)是R上凹函数.已知二次函数f(x)=ax2+x(a∈R,且a≠0).(1)求证:当a>0时,函数f(x)的凹函数;
(2)如果x∈[0,1]时,|f(x)|≤1,试求a的取值范围.
【答案】分析:(1)利用函数f(x)的解析式,根据凹函数定义即可验证;
(2)由|f(x)|≤1表示出关于a的不等式,利用分离参数法,根据x的取值范围进行分析可得答案.
解答:(1)证明:∵二次函数f(x)=ax2+x
∴任取x1,x2∈R,则 =a(
=a( )2+
)2+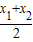 -
- (
( +
+ )=-
)=-
∵a>0, ,∴
,∴
∴
∴
∴当a>0时,函数f(x)的凹函数;
(2)解:由-1≤f(x)=ax2+x≤1,则有ax2≥-x-1且ax2≤-x+1.
(i)若x=0时,则a∈R恒成立,
(ii)若x∈(0,1]时,有 a≥- -
- 且a≤-
且a≤-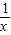 +
+
∴a≥- -
- =-(
=-( +
+ )2+
)2+ 且a≤-
且a≤-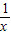 +
+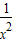 =(
=( -
- )2-
)2- ,
,
∵0<x≤1,∴ ≥1.
≥1.
∴当 =1时,-(
=1时,-( +
+ )2+
)2+ 的最大值为-(1+
的最大值为-(1+ )2+
)2+ =-2,(
=-2,( -
- )2-
)2- 的最小值为(1-
的最小值为(1- )2-
)2- =0
=0
∴0≥a≥-2.
综(i)(ii)知,0≥a≥-2
点评:本题考查新定义--凹函数,考查学生对新定义的理解,考查恒成立问题,考查分离参数法的运用,属于中档题.
(2)由|f(x)|≤1表示出关于a的不等式,利用分离参数法,根据x的取值范围进行分析可得答案.
解答:(1)证明:∵二次函数f(x)=ax2+x
∴任取x1,x2∈R,则
 =a(
=a( )2+
)2+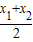 -
- (
( +
+ )=-
)=-
∵a>0,
 ,∴
,∴
∴

∴

∴当a>0时,函数f(x)的凹函数;
(2)解:由-1≤f(x)=ax2+x≤1,则有ax2≥-x-1且ax2≤-x+1.
(i)若x=0时,则a∈R恒成立,
(ii)若x∈(0,1]时,有 a≥-
 -
- 且a≤-
且a≤-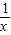 +
+
∴a≥-
 -
- =-(
=-( +
+ )2+
)2+ 且a≤-
且a≤-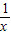 +
+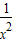 =(
=( -
- )2-
)2- ,
,∵0<x≤1,∴
 ≥1.
≥1.∴当
 =1时,-(
=1时,-( +
+ )2+
)2+ 的最大值为-(1+
的最大值为-(1+ )2+
)2+ =-2,(
=-2,( -
- )2-
)2- 的最小值为(1-
的最小值为(1- )2-
)2- =0
=0∴0≥a≥-2.
综(i)(ii)知,0≥a≥-2
点评:本题考查新定义--凹函数,考查学生对新定义的理解,考查恒成立问题,考查分离参数法的运用,属于中档题.

练习册系列答案
相关题目