题目内容
20、已知定义在R上的函数f(x)=-2x3+bx2+cx(b,c∈R),函数F(x)=f(x)-3x2是奇函数,函数f(x)在x=-1处取极值.
(1)求f(x)的解析式;
(2)讨论f(x)在区间[-3,3]上的单调性.
(1)求f(x)的解析式;
(2)讨论f(x)在区间[-3,3]上的单调性.
分析:(1)通过函数F(x)是奇函数先求出b,在利用函数f(x)在x=-1处取极值可得f′(-1)=0求得c,则函数解析式求得.
(2)先求导数fˊ(x),在区间[-3,3]内解不等式fˊ(x)>0和fˊ(x)<0即可.
(2)先求导数fˊ(x),在区间[-3,3]内解不等式fˊ(x)>0和fˊ(x)<0即可.
解答:解:(1)∵函数F(x)=f(x)-3x2是奇函数,
∴F(-x)=-F(x),化简计算得b=3.
∵函数f(x)在x=-1处取极值,∴f′(x)=0.
f(x)=-2x3+3x2+cx,f′(x)=-6x2+6x+c
∴f′(-1)=-6-6+c=0,c=12.
∴f(x)=-2x3+3x2+12x,
(2)f′(x)=-6x2+6x+12=-6(x2-x-2).
令f′(x)=0,得x1=-1,x2=2,
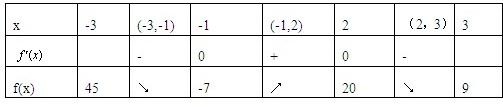
∴函数f(x)在[-3,-1]和[2,3]上是减函数,
函数f(x)在[-1,2]上是增函数.
∴F(-x)=-F(x),化简计算得b=3.
∵函数f(x)在x=-1处取极值,∴f′(x)=0.
f(x)=-2x3+3x2+cx,f′(x)=-6x2+6x+c
∴f′(-1)=-6-6+c=0,c=12.
∴f(x)=-2x3+3x2+12x,
(2)f′(x)=-6x2+6x+12=-6(x2-x-2).
令f′(x)=0,得x1=-1,x2=2,

∴函数f(x)在[-3,-1]和[2,3]上是减函数,
函数f(x)在[-1,2]上是增函数.
点评:本题考查了待定系数法求解析式,利用导数研究函数的单调性,属于基础题.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
已知定义在R上的函数f(x),对任意x∈R,都有f(x+6)=f(x)+f(3)成立,若函数y=f(x+1)的图象关于直线x=-1对称,则f(2013)=( )
| A、0 | B、2013 | C、3 | D、-2013 |