题目内容
【题目】A城市的出租车计价方式为:若行程不超过3千米,则按“起步价”10元计价;若行程超过3千米,则之后2千米以内的行程按“里程价”计价,单价为1.5元/千米;若行程超过5千米,则之后的行程按“返程价”计价,单价为2.5元/千米.设某人的出行行程为x千米,现有两种乘车方案:①乘坐一辆出租车;②每5千米换乘一辆出租车.
(Ⅰ)分别写出两种乘车方案计价的函数关系式;
(Ⅱ)对不同的出行行程,①②两种方案中哪种方案的价格较低?请说明理由.
【答案】解:(Ⅰ)方案①计价的函数为f(x),方案②计价的函数为g(x),
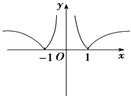
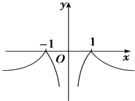
则f(x)= 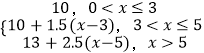 ;
;
g(x)= ![]() ;
;
(Ⅱ)当0<x≤5时,f(x)=g(x),
x>5时,f(x)<g(x)即方案①的价格比方案②的价格低,
理由如下:
x∈(5k,5k+3)(k∈N),f(x)﹣g(x)=2.5x﹣13k﹣9.5≤﹣0.5k﹣2<0;
x∈(5k+3,5k+5)(k∈N),f(x)﹣g(x)=x﹣5.5k﹣5≤﹣0.5k<0.
【解析】(1)、由题意可得分段函数的解析式。
(2)、由题意可得当0<x≤5时,f(x)=g(x),x>5时,f(x)<g(x)即方案①的价格比方案②的价格低,由解析式可得。

练习册系列答案
相关题目