题目内容
【题目】已知椭圆![]() 的左右焦点分别为
的左右焦点分别为![]() ,左顶点为
,左顶点为![]() ,且
,且![]() ,
,![]() 是椭圆上一点.
是椭圆上一点.
(1)求椭圆![]() 的方程;
的方程;
(2)若直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,直线
两点,直线![]() 别与
别与![]() 轴交于点
轴交于点![]() ,求证:在
,求证:在![]() 轴上存在点
轴上存在点![]() ,使得无论非零实数
,使得无论非零实数![]() 怎样变化,以
怎样变化,以![]() 为直径的圆都必过点
为直径的圆都必过点![]() ,并求出点
,并求出点![]() 的坐标.
的坐标.
【答案】(1)![]() ;(2)证明详见解析,点P坐标为
;(2)证明详见解析,点P坐标为![]() 或
或![]() .
.
【解析】
(1)依题意得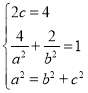 ,解出即可;
,解出即可;
(2)假设存在这样的点P,设![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,
联立直线与椭圆方程求得点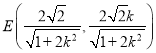 ,进而求出直线
,进而求出直线![]() 的方程
的方程![]() ,由此可得
,由此可得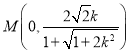 ,同理可得
,同理可得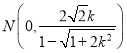 ,由此可得
,由此可得![]() ,解出即可得出结论.
,解出即可得出结论.
(1)解:依题意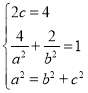 ,解得
,解得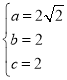 ,
,
∴椭圆方程为![]() ;
;
(2)证:假设存在这样的点P,设![]() ,
,![]() ,
,![]() ,则
,则![]() ,
,
联立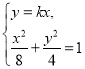 ,消去
,消去![]() ,得
,得![]() ,
,
解得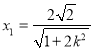 ,
,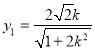 ,即
,即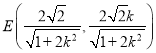 ,
,
∵![]() ,
,
∴直线![]() 的斜率
的斜率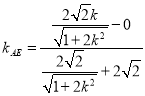
![]() ,
,
∴直线![]() 的方程为
的方程为![]() ,
,
可得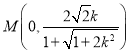 ,
,
同理可得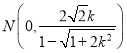 ,
,
∴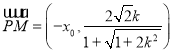 ,
,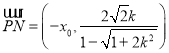 ,
,
则![]() ,解得
,解得![]() 或
或![]() ,
,
∴存在点![]() 且坐标为
且坐标为![]() 或
或![]() ,使得无论非零实数
,使得无论非零实数![]() 怎么变化,以
怎么变化,以![]() 为直径的圆都必过点
为直径的圆都必过点![]() .
.

 活力试卷系列答案
活力试卷系列答案 课课优能力培优100分系列答案
课课优能力培优100分系列答案【题目】在全面建成小康社会的决胜阶段,让贫困地区同全国人民共同进入全面小康社会是我们党的庄严承诺.在“脱真贫、真脱贫”的过程中,精准扶贫助推社会公平显得尤其重要.若某农村地区有200户贫困户,经过一年扶贫后,对该地区的“精准扶贫”的成效检查验收.从这200户贫困户中随机抽出50户,对各户的人均年收入(单位:千元)进行调查得到如下频数表:
人均年收入 |
|
|
|
|
|
|
频数 | 2 | 3 | 10 | 20 | 10 | 5 |
若人均年收入在4000元以下的判定为贫困户,人均年收入在4000元~8000元的判定为脱贫户,人均年收入达到8000元的判定为小康户.
(1)用样本估计总体,估计该地区还有多少户没有脱贫;
(2)为了了解未脱贫的原因,从抽取的50户中用分层抽样的方法抽10户进行调研.
①贫困户、脱贫户、小康户分别抽到的人数是多少?
②从被抽到的脱贫户和小康户中各选1人做经验介绍,求小康户中人均年收入最高的一户被选到的概率.
【题目】某市实验中学数学教研组,在高三理科一班进行了一次“采用两种不同方式进行答卷”的考试实验,第一种做卷方式:按从前往后的顺序依次做;第二种做卷方式:先做简单题,再做难题.为了比较这两种做卷方式的效率,选取了![]() 名学生,将他们随机分成两组,每组
名学生,将他们随机分成两组,每组![]() 人.第一组学生用第一种方式,第二组学生用第二种方式,根据学生的考试分数(单位:分)绘制了茎叶图如图所示.
人.第一组学生用第一种方式,第二组学生用第二种方式,根据学生的考试分数(单位:分)绘制了茎叶图如图所示.
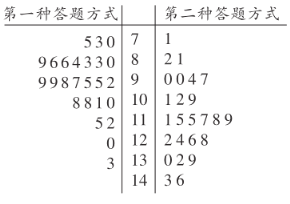
![]() 若
若![]() 分(含
分(含![]() 分)以上为优秀,根据茎叶图估计两种做卷方式的优秀率;
分)以上为优秀,根据茎叶图估计两种做卷方式的优秀率;
![]() 设
设![]() 名学生考试分数的中位数为
名学生考试分数的中位数为![]() ,根据茎叶图填写下面的
,根据茎叶图填写下面的![]() 列联表:
列联表:
超过中位数 | 不超过中位数 | 合计 | |
第一种做卷方式 | |||
第一种做卷方式 | |||
合计 |
根据列联表,能否有![]() 的把握认为两种做卷方式的效率有差异?
的把握认为两种做卷方式的效率有差异?
附: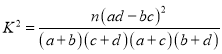 ,
,![]() .
.
|
|
|
|
|
|
|
|