Question

【题目】在正方体ABCD﹣A1B1C1D1中，点E，F分别为棱BC，CC1的中点，过点A，E，F作平面截正方体的表面所得图形是（ ）

A.三角形B.平行四边形C.等腰梯形D.平面五边形

Answer 1

【答案】C

【解析】

连接AD1，BC1，D1F，由正方体的性质可得EF//BC1//AD1，且EFBC1AD1，进而可得平面截正方体的表面所得图形为四边形A D1FE，，再根据正方体性质可求得AE＝D1F，即可得解.

连接AD1，BC1，D1F如图：

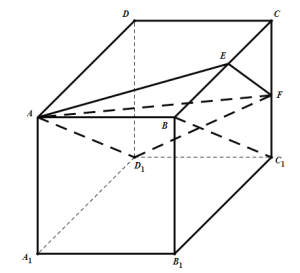
由点E，F分别为棱BC，CC1的中点可得EF//BC1//AD1，且，

所以平面AEF与平面A D1FE为同一平面，

则平面截正方体的表面所得图形为四边形A D1FE，即所得截面图形是梯形，

设正方体棱长为2a，则，

因此所得截面图形是等腰梯形，

故选：C.