题目内容
已知等差数列{an}的首项a1=1,公差d>0,且第2项,第5项,第14项分别是等比数列{bn}的第2项,第3项,第4项.
(1)求数列{an}与{bn}的通项公式;
(2)求数列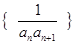 的前n项和
的前n项和
(3)设数列{cn}对任意自然数n,均有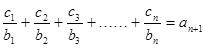 ,求c1+c2+c3+……+c2006值.
,求c1+c2+c3+……+c2006值.
(1)求数列{an}与{bn}的通项公式;
(2)求数列
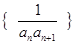 的前n项和
的前n项和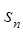
(3)设数列{cn}对任意自然数n,均有
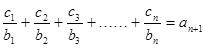 ,求c1+c2+c3+……+c2006值.
,求c1+c2+c3+……+c2006值.(1)an=2n-1,bn=3n-1.(2)见解析
(3)当n=1时,c1="3" 当n≥2时,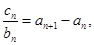
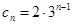 ,
,
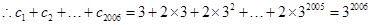
(3)当n=1时,c1="3" 当n≥2时,
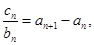
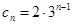 ,
,
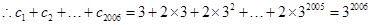
试题分析:(1)利用等差数列的通项公式将第二项,第五项,第十四项用{an}的首项与公差表示,再据此三项成等比数列,列出方程,求出公差,利用等差数列及等比数列的通项公式求出数列{an}与{bn}的通项公式.
(2)根据数列的通项公式通过裂项求解数列的和
(3)当n≥2时,根据an+1-an,求出数列{cn}通项公式,但当n=1时,不符合上式,因此数列{cn}是分段数列;然后根据通项公式即可求出结果
解:(1)由题意得(a1+d)(a1+13d)=(a1+4d)2(d>0) 解得d=2,∴an=2n-1,bn=3n-1.
(3)当n=1时,c1="3" 当n≥2时,
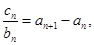
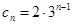 ,
,

点评:解决该试题的关键是对于等差数列,等比数列基本关系式的求解和运用。

练习册系列答案
相关题目
 中,
中,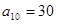 ,
,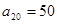 .
.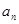 ;
;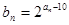 ,证明:数列
,证明:数列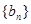 为等比数列;
为等比数列;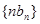 的前
的前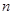 项和
项和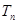 .
.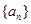 中,
中,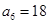 且
且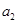 是
是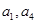 的等比中项,则它的第4项到第11项的和为
的等比中项,则它的第4项到第11项的和为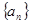 中,
中,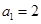 ,
,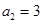 ,其前
,其前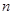 项和
项和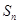 满足
满足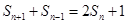 (
(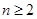 ,
,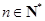 ).
).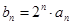 , 求数列
, 求数列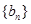 的前
的前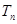 ;
;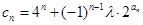 (
(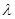 为非零整数,
为非零整数,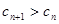 恒成立.
恒成立.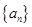 满足:
满足: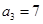 ,
,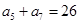 ,
,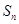 .
.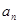 及;
及;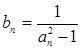 (n
(n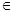 N*),求数列
N*),求数列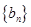 的前n项和
的前n项和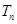 .
. 中,已知
中,已知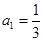 ,
,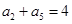 ,
,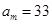 ,则m为______________.
,则m为______________.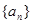 是非零等差数列,又
是非零等差数列,又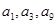 组成一个等比数列的前三项,则
组成一个等比数列的前三项,则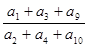 的值是 .
的值是 .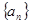 满足:
满足: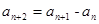 (
(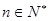 ),且
),且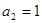 ,若数列的前2011项之
,若数列的前2011项之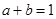 ,
,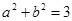 ,
,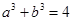 ,
,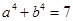 ,
, ,
,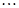 则
则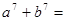 ( )
( )