��Ŀ����
12��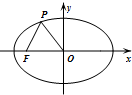 ��ͼ����֪��ԲC������Ϊԭ��O��F��-2$\sqrt{5}$��0��ΪC���㣬PΪC��һ�㣬����|OP|=|OF|��|PF|=4������ԲC�ķ���Ϊ��������
��ͼ����֪��ԲC������Ϊԭ��O��F��-2$\sqrt{5}$��0��ΪC���㣬PΪC��һ�㣬����|OP|=|OF|��|PF|=4������ԲC�ķ���Ϊ��������| A�� | $\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{5}$=1 | B�� | $\frac{{x}^{2}}{30}$+$\frac{{y}^{2}}{10}$=1 | C�� | $\frac{{x}^{2}}{36}$+$\frac{{y}^{2}}{16}$=1 | D�� | $\frac{{x}^{2}}{45}$+$\frac{{y}^{2}}{25}$=1 |
���� ����Բ���ҽ���ΪF�䣬��|OP|=|OF|����Բ�ĶԳ���֪����PFF��Ϊֱ�������Σ��ɹ��ɶ�������|PF��|������Բ�Ķ��壬��a2����b2=a2-c2����b2��Ȼ�������Բ�����̵���ʽ��ֱ��д����Բ�ķ��̣�
��� 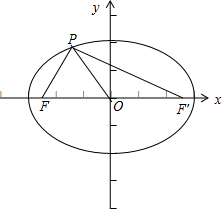 �⣺������ɵ�c=2$\sqrt{5}$�����ҽ���ΪF�䣬��|OP|=|OF|=|OF��|֪����PFF��=��FPO����OF��P=��OPF�䣬
�⣺������ɵ�c=2$\sqrt{5}$�����ҽ���ΪF�䣬��|OP|=|OF|=|OF��|֪����PFF��=��FPO����OF��P=��OPF�䣬
���ԡ�PFF��+��OF��P=��FPO+��OPF�䣬
�ɡ�PFF��+��OF��P+��FPO+��OPF��=180��֪����FPO+��OPF��=90�㣬��PF��PF�䣮
��Rt��PFF���У��ɹ��ɶ�������|PF��|=$\sqrt{{FF��}^{2}{-PF}^{2}}$=$\sqrt{{��4\sqrt{5}��}^{2}{-4}^{2}}$=8��
����Բ���壬��|PF|+|PF��|=2a=4+8=12���Ӷ�a=6����a2=36��
���� b2=a2-c2=36-${��2\sqrt{5}��}^{2}$=16��
������Բ�ķ���Ϊ$\frac{{x}^{2}}{36}$+$\frac{{y}^{2}}{16}$=1��
��ѡ��C��
���� �����������⣬��Ҫ��������Բ�Ķ��弰�伸��������������Բ�����̵���⣬�ؼ��Ǹ��������ͼ�εļ����������г�����a��b��c���������̣���������ȷ��a2��b2�������е��⣮

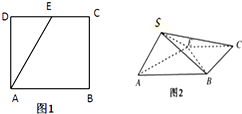 ��ͼ����EΪ������ABCD��CD�����ڵ�C��D�Ķ��㣬����ADE��AE���۳ɡ�SAE��ʹ��ƽ��SAE��ƽ��ABCE������������˵������ȷ�ĸ����ǣ�������
��ͼ����EΪ������ABCD��CD�����ڵ�C��D�Ķ��㣬����ADE��AE���۳ɡ�SAE��ʹ��ƽ��SAE��ƽ��ABCE������������˵������ȷ�ĸ����ǣ�������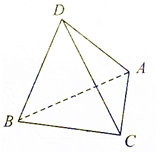 ��ͼ��A��B��C��DΪ�ռ��ĵ㣬��ABC�У�AB=AC=BC=2���ȱ�������ADB��ABΪ���˶�����ƽ��ADB��ƽ��ABCʱ����CD=$\sqrt{6}$��
��ͼ��A��B��C��DΪ�ռ��ĵ㣬��ABC�У�AB=AC=BC=2���ȱ�������ADB��ABΪ���˶�����ƽ��ADB��ƽ��ABCʱ����CD=$\sqrt{6}$��