题目内容
2．已知x，y∈（0，2），则$\sqrt{{x^2}+{y^2}}+\sqrt{{x^2}+{{（y-2）}^2}}+\sqrt{{{（x-2）}^2}+{y^2}}+\sqrt{{{（x-2）}^2}+{{（y-2）}^2}}$的最小值为4$\sqrt{2}$．分析 直接利用四个和式的几何意义求得答案．
解答 解：$\sqrt{{x}^{2}+{y}^{2}}$表示点（x，y）与原点（0，0）之间的距离，
$\sqrt{{x}^{2}+（y-2）^{2}}$表示点（x，y）与点（0，2）之间的距离，
$\sqrt{（x-2）^{2}+{y}^{2}}$表示点（x，y）与点（2，0）之间的距离，
$\sqrt{（x-2）^{2}+（y-2）^{2}}$表示点（x，y）与点（2，2）之间的距离，
∴函数就是四个距离之和，
满足条件0＜x＜2，0＜y＜2的点（x，y）位于矩形内，
则距离之和的最小值就是此矩形的对角线长的2倍，等于4$\sqrt{2}$．
故答案为：4$\sqrt{2}$．
点评 本题考查了函数值的求法，考查了数学转化思想方法，关键是转化为几何意义，是中档题．
练习册系列答案
阅读快车系列答案
相关题目
13．设全集为R，集合A={x|x2-x-2≤0}，B={x|x≥0}，则A∩∁RB=（ ）
| A． | [-1，0） | B． | [-2，0） | C． | [0，1] | D． | [0，2] |
10．已知$\overrightarrow a=（3x，2），\overrightarrow b=（6，1）$，若$\overrightarrow a∥\overrightarrow b$，则实数x=（ ）
| A． | 4 | B． | $\frac{1}{4}$ | C． | 9 | D． | $\frac{1}{9}$ |
7．正弦函数y=sin（x+$\frac{3π}{2}$），x∈R的图象关于（ ）对称．
| A． | y轴 | B． | 直线x=$\frac{3π}{2}$ | C． | 直线x=$\frac{π}{2}$ | D． | 直线x=-$\frac{π}{2}$ |
14．设m＞n，函数y=（x-m）2（n-x）的图象可能是（ ）
| A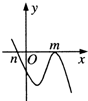． |  | B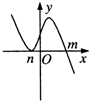． |  | C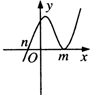． |  | D． |  |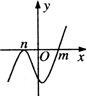
11．角θ的终边与单位圆的交点的横坐标为$-\frac{1}{2}$，则tanθ的值为（ ）
| A． | $-\sqrt{3}$ | B． | ±1 | C． | $±\sqrt{3}$ | D． | $±\frac{{\sqrt{3}}}{3}$ |
12．
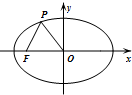如图，已知椭圆C的中心为原点O，F（-2$\sqrt{5}$，0）为C的左焦点，P为C上一点，满足|OP|=|OF|且|PF|=4，则椭圆C的方程为（ ）
如图，已知椭圆C的中心为原点O，F（-2$\sqrt{5}$，0）为C的左焦点，P为C上一点，满足|OP|=|OF|且|PF|=4，则椭圆C的方程为（ ）| A． | $\frac{{x}^{2}}{25}$+$\frac{{y}^{2}}{5}$=1 | B． | $\frac{{x}^{2}}{30}$+$\frac{{y}^{2}}{10}$=1 | C． | $\frac{{x}^{2}}{36}$+$\frac{{y}^{2}}{16}$=1 | D． | $\frac{{x}^{2}}{45}$+$\frac{{y}^{2}}{25}$=1 |