题目内容
已知
=(2sinx,m),
=(sinx+cosx,1),函数f(x)=
•
(x∈R),若f(x)的最大值为
.
(1)求m的值;
(2)若将f(x)的图象向左平移n(n>0)个单位后,关于y轴对称,求n的最小值.
| a |
| b |
| a |
| b |
| 2 |
(1)求m的值;
(2)若将f(x)的图象向左平移n(n>0)个单位后,关于y轴对称,求n的最小值.
(1)f(x)=
•
=2sin2x+2sinxcosx+m
=1-cos2x+sin2x+m
=
sin(2x-
)+m+1
∵f(x)的最大值为
,而
sin(2x-
)最大值是
,m+1是常数
∴m+1=0,m=-1
(2)由(1)知,f(x)=
sin(2x-
),将其图象向左平移n个单位,
对应函数为y=
sin[2(x+n)-
]
平移后函数图象关于y轴对称,则该函数为偶函数,表达式的一般形式是
y=
sin(2x+
+kπ)(k∈Z)
要使n取最小正数,则对应函数为y=
sin(2x+
),
此时n=
| a |
| b |
=2sin2x+2sinxcosx+m
=1-cos2x+sin2x+m
=
| 2 |
| π |
| 4 |
∵f(x)的最大值为
| 2 |
| 2 |
| π |
| 4 |
| 2 |
∴m+1=0,m=-1
(2)由(1)知,f(x)=
| 2 |
| π |
| 4 |
对应函数为y=
| 2 |
| π |
| 4 |
平移后函数图象关于y轴对称,则该函数为偶函数,表达式的一般形式是
y=
| 2 |
| π |
| 2 |
要使n取最小正数,则对应函数为y=
| 2 |
| π |
| 2 |
此时n=
| 3π |
| 8 |

练习册系列答案
相关题目
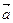 =(3,1),
=(3,1),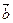 =(x,-3),且
=(x,-3),且