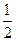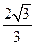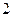题目内容
已知向量
=(cosα,sinα),
=(cosβ,sinβ),若|
-
|=
,则
和
的夹角为( )
| a |
| b |
| a |
| b |
| 2 |
| a |
| b |
| A.60° | B.90° | C.120° | D.150° |
∵向量
=(cosα,sinα),
=(cosβ,sinβ),
∴|
|=
=1,|
|=
=1.
∵|
-
|=
,
∴
=
,
∴2-2cos<
,
>=2,
解得cos<
,
>=0,
∴<
,
>=90°.
故选:B.
| a |
| b |
∴|
| a |
| cos2α+sin2α |
| b |
| cos2β+sin2β |
∵|
| a |
| b |
| 2 |
∴
|
| 2 |
∴2-2cos<
| a |
| b |
解得cos<
| a |
| b |
∴<
| a |
| b |
故选:B.

练习册系列答案
 53天天练系列答案
53天天练系列答案
相关题目
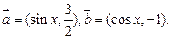
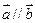 时,求
时,求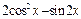 的值;(2)求
的值;(2)求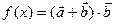 在
在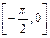 上的值域.
上的值域.
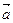 =(-4,3),
=(-4,3),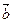 =(5,6),则
=(5,6),则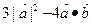 等于( )
等于( )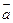 与向量
与向量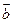 的夹角为
的夹角为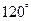 ,若向量
,若向量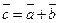 ,且
,且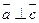 ,
,
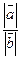 的值为 ( )
的值为 ( )