题目内容
如果随机变量ξ~N(0,σ2),且P(-2<ξ≤0)="0.4" ,则P(ξ>2)等于:
| A.0.1 | B.0.2 | C.0.3 | D.0.4 |
A
解析试题分析:本题考查正态分布曲线的性质,随机变量ξ服从正态分布N(0,σ2),由此知曲线的对称轴为Y轴,|ξ|>2包括了两部分ξ>2或ξ<-2由此可得P(|ξ|>2)=1-P(-2≤ξ≤2),再由P(-2≤ξ≤0)=0.4,答案易解:∵随机变量ξ服从正态分布N(0,σ2),且P(-2≤ξ≤0)=0.4,∴P(-2≤ξ≤2)=0.8,∴P(|ξ|>2)=1-P(-2≤ξ≤2)=1-0.8=0.2,故P(ξ>2)=0.1选A
考点:正态分布
点评:本题考查正态分布曲线的重点及曲线所表示的意义,解题的关键是正确正态分布曲线的重点及曲线所表示的意义,由曲线的对称性求出概率,本题是一个数形结合的题,识图很重要

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案
相关题目
甲乙两人玩猜数字游戏,先由甲在心中任想一个数字,记为 ,再由乙猜甲刚才所想的数字,把乙猜的数字记为
,再由乙猜甲刚才所想的数字,把乙猜的数字记为 ,且
,且 。若
。若 ,则称甲乙“心有灵犀”。现任意找两人玩这个游戏,得出他们“心有灵犀”的概率为 ( )
,则称甲乙“心有灵犀”。现任意找两人玩这个游戏,得出他们“心有灵犀”的概率为 ( )
A. | B. | C. | D. |
设函数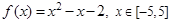 .若从区间
.若从区间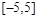 内随机选取一个实数
内随机选取一个实数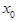 ,则所选取的实数
,则所选取的实数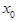 满足
满足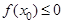 的概率为( )
的概率为( )
A.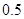 | B.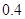 | C.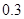 | D.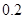 |
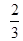 ,则阴影区域的面积为( )
,则阴影区域的面积为( ) 









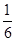
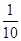

 ( )
( )


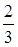
 )等于( )
)等于( )


