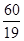题目内容
现有编号为1—5的5名学生到电脑上查阅学习资料,而机房只有编号为1—4的4台电脑可供使用,因此,有两位学生必须共用同一台电脑,而其他三位学生每人使用一台,则恰有2位学生的编号与其使用的电脑编号相同的概率为( )
A. | B.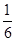 | C.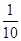 | D. |
A
解析试题分析: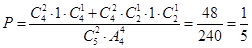 , 故选A.
, 故选A.
注:
式子的分母是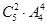 是所有可能情况,即5个人里面选2个人做一堆即
是所有可能情况,即5个人里面选2个人做一堆即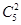 ,然后将剩余的3人和选好的两人共4堆做全排列即
,然后将剩余的3人和选好的两人共4堆做全排列即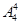 对应于4台电脑的位置,所以是
对应于4台电脑的位置,所以是
分子是根据编号为5的同学来分成两种情况:
(1)编号为5的同学和另外4人中的一人共用一台电脑.那么可以先将1到4编号的同学排好,再将某台电脑给编号5的同学共用。即是先从4台电脑里面选择两台,这两台编号与使用者编号相同,共有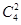 种,剩下的两台电脑和两名同学的配对关系则是固定的,即有
种,剩下的两台电脑和两名同学的配对关系则是固定的,即有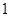 种,然后是给5号同学选择电脑
种,然后是给5号同学选择电脑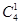 种,所以是
种,所以是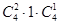 种.
种.
(2)编号为5的同学单独使用一台电脑。那么是先从4台电脑里面选择两台,这两台编号与使用者编号相同,共有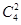 种,在剩下的两台电脑里面选择一台给5号同学单独使用,即有
种,在剩下的两台电脑里面选择一台给5号同学单独使用,即有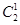 种,则最后一台电脑的使用者是固定的,再将最后一位同学放入先前编号与使用者编号相同的两台电脑中,即有
种,则最后一台电脑的使用者是固定的,再将最后一位同学放入先前编号与使用者编号相同的两台电脑中,即有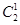 种,所以是
种,所以是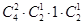 种.
种.
所以总共的情况是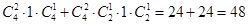 种.
种.
考点:古典概型概率的计算,简单排列组合应用问题。
点评:中档题,古典概型概率的计算,关键是明确“事件数”,根据题目的条件,利用排列组合知识计算是常见方法。有时利用“树图法”、“坐标法”,更为直观。

如果随机变量ξ~N(0,σ2),且P(-2<ξ≤0)="0.4" ,则P(ξ>2)等于:
| A.0.1 | B.0.2 | C.0.3 | D.0.4 |
在区间 内任取两个实数,则这两个实数的和大于
内任取两个实数,则这两个实数的和大于 的概率为( )
的概率为( )
A. | B. | C. | D. |
某学生解选择题出错的概率为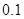 ,该生解三道选择题至少有一道出错的概率是( )
,该生解三道选择题至少有一道出错的概率是( )
A.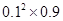 | B.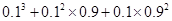 |
C.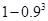 | D.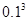 |
设随机变量 的分布列为
的分布列为 ,则
,则 ( )
( )
A. | B. | C. | D. |
在区间 上随机取一实数
上随机取一实数 ,则该实数
,则该实数 满足不等式
满足不等式 的概率为( )
的概率为( )
A. | B. | C. | D. |




 和
和 , 甲、乙两人各射击一次,目标被命中的概率为:
, 甲、乙两人各射击一次,目标被命中的概率为:


 小时,种植一棵枫树苗用时
小时,种植一棵枫树苗用时 小时.完成这次植树任务需要最短时间为( )
小时.完成这次植树任务需要最短时间为( )