题目内容
如图所示,边长为2的正方形中有一封闭曲线围成的阴影区域,在正方形中随机撒一粒豆子,它落在阴影区域内的概率是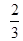 ,则阴影区域的面积为( )
,则阴影区域的面积为( ) 
A. | B. | C.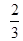 | D.无法计算 |
B
解析试题分析:正方形中随机撒一粒豆子,它落在阴影区域内的概率, ,又因为
,又因为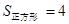 ,所以
,所以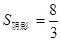 ,故选B.
,故选B.
考点:几何概型
点评:利用几何概型的意义进行模拟试验,估算不规则图形面积的大小,关键是要根据几何概型的计算公式,探究不规则图形面积与已知的规则图形的面积之间的关系,及它们与模拟试验产生的概率(或频数)之间的关系,并由此列出方程,解方程即可得到答案.

练习册系列答案
相关题目
如果随机变量ξ~N(0,σ2),且P(-2<ξ≤0)="0.4" ,则P(ξ>2)等于:
| A.0.1 | B.0.2 | C.0.3 | D.0.4 |
在区间 上随机取一实数
上随机取一实数 ,则该实数
,则该实数 满足不等式
满足不等式 的概率为( )
的概率为( )
A. | B. | C. | D. |




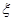 和
和 ,其中
,其中 ,且
,且 ,若
,若 的值为
的值为


 B.
B. C.
C. D.
D.
 ,
, =
=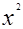 +
+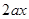 -
- +
+

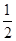

 和
和 , 甲、乙两人各射击一次,目标被命中的概率为:
, 甲、乙两人各射击一次,目标被命中的概率为: