Question

【题目】已知函数f(x)= ,x∈[-1,1],函数g(x)=[f(x)]2-2af(x)+3的最小值为h(a).

(1)求h(a).

(2)是否存在实数m>n>3,当h(a)的定义域为[n,m]时,值域为[n2,m2]?若存在,求出m,n的值;若不存在,说明理由.

Answer 1

【答案】(1) h(a)= 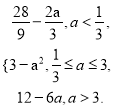(2) 满足题意的m,n不存在.

【解析】(1)∵x∈[－1,1]，∴f(x)＝∈.设t＝，t∈，

则y＝φ(t)＝t2－2at＋3＝(t－a)2＋3－a2.

当a＜时，ymin＝h(a)＝φ＝；

当≤a≤3时，ymin＝h(a)＝φ(a)＝3－a2；

当a＞3时，ymin＝h(a)＝φ(3)＝12－6a.

∴h(a)＝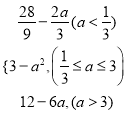

(2)假设满足题意的m、n存在，∵m＞n＞3，∴h(a)＝12－6a在(3，＋∞)上是减函数．∵h(a)的定义域为[n，m]，值域为[n2，m2]，∴，由②－①得6(m－n)＝(m－n)(m＋n)，∵m＞n＞3，∴m＋n＝6，但这与“m＞n＞3”矛盾，∴满足题意的m、n不存在．