题目内容
已知曲线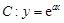 .
.
(1)若曲线C在点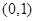 处的切线为
处的切线为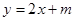 ,求实数
,求实数 和
和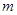 的值;
的值;
(2)对任意实数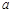 ,曲线
,曲线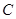 总在直线
总在直线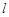 :
: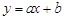 的上方,求实数
的上方,求实数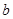 的取值范围.
的取值范围.
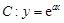 .
.(1)若曲线C在点
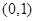 处的切线为
处的切线为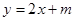 ,求实数
,求实数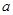 和
和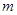 的值;
的值;(2)对任意实数
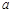 ,曲线
,曲线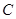 总在直线
总在直线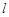 :
: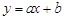 的上方,求实数
的上方,求实数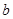 的取值范围.
的取值范围.(1) ,
, ,(2)
,(2)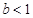 .
.
 ,
, ,(2)
,(2)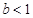 .
.试题分析:(1)根据导数几何意义,所以
 .因为
.因为 ,所以
,所以 .因为
.因为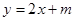 过点
过点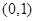 ,所以
,所以 ,(2)由题意得:不等式
,(2)由题意得:不等式 恒成立,恒成立问题一般转化为最值问题.一是分类讨论求函数
恒成立,恒成立问题一般转化为最值问题.一是分类讨论求函数 最小值,二是变量分离为
最小值,二是变量分离为 恒成立,求函数
恒成立,求函数 最小值.两种方法都是
最小值.两种方法都是 ,然后对实数a进行讨论,当
,然后对实数a进行讨论,当 时,
时,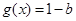 ,所以
,所以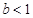 .当
.当 时,由
时,由 得
得 ,不论
,不论 还是
还是 ,
, 都是先减后增,即
都是先减后增,即 的最小值为
的最小值为 ,所以
,所以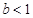 .
.试题解析:解
(1)
 , 2分
, 2分因为曲线C在点(0,1)处的切线为L:
 ,
,所以
 且
且 . 4分
. 4分解得
 ,
, -5分
-5分(2)法1:
对于任意实数a,曲线C总在直线的
 的上方,等价于
的上方,等价于?x,
 ,都有
,都有 ,
,即?x,
 R,
R, 恒成立, 6分
恒成立, 6分令
 , 7分
, 7分①若a=0,则
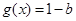 ,
,所以实数b的取值范围是
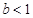 ; 8分
; 8分②若
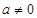 ,
, ,
,由
 得
得 , 9分
, 9分 的情况如下:
的情况如下: |  | 0 |  |
 |  | 0 | + |
 |  | 极小值 |  |
所以
 的最小值为
的最小值为 , 12分
, 12分所以实数b的取值范围是
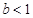 ;
;综上,实数b的取值范围是
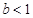 . 13分
. 13分法2:对于任意实数a,曲线C总在直线的
 的上方,等价于
的上方,等价于?x,
 ,都有
,都有 ,即
,即?x,
 R,
R, 恒成立, 6分
恒成立, 6分令
 ,则等价于?
,则等价于? ,
, 恒成立,
恒成立,令
 ,则
,则 , 7分
, 7分由
 得
得 , 9分
, 9分 的情况如下:
的情况如下: |  | 0 |  |
 |  | 0 | + |
 |  | 极小值 |  |
所以
 的最小值为
的最小值为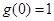 , 12分
, 12分实数b的取值范围是
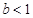 . 13分
. 13分
练习册系列答案
 学而优暑期衔接南京大学出版社系列答案
学而优暑期衔接南京大学出版社系列答案 Happy holiday欢乐假期暑假作业广东人民出版社系列答案
Happy holiday欢乐假期暑假作业广东人民出版社系列答案 快乐暑假暑假能力自测中西书局系列答案
快乐暑假暑假能力自测中西书局系列答案
相关题目
 的极值
的极值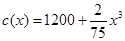 (万元),已知产品单价P(万元)与产品件数x满足:
(万元),已知产品单价P(万元)与产品件数x满足: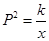 ,生产100件这样的产品单价为50万元,产量定为多少件时总利润最大?
,生产100件这样的产品单价为50万元,产量定为多少件时总利润最大?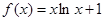
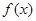 在
在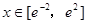 上的最大值与最小值;
上的最大值与最小值;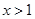 时,函数
时,函数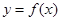 的图像恒在直线
的图像恒在直线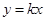 上方,求实数
上方,求实数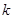 的取值范围;
的取值范围;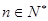 时,
时,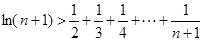 .
.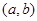 ,其中
,其中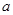 表示第一次抛掷的结果,
表示第一次抛掷的结果,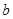 表示第二次抛掷的结果,则函数
表示第二次抛掷的结果,则函数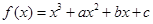 有极值点的概率为( )
有极值点的概率为( )



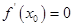 是
是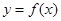 在
在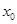 处取得极值的既不充分也不必要条件;
处取得极值的既不充分也不必要条件;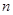 项和
项和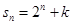 ,则必有
,则必有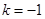 ;
;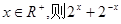 的最小值为2;
的最小值为2;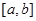 上必定有最大值、最小值;
上必定有最大值、最小值;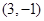 的距离等于到定直线
的距离等于到定直线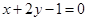 的距离的点的轨迹是抛物线.
的距离的点的轨迹是抛物线.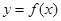 的导函数存在,则函数
的导函数存在,则函数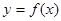 在一点的导数值为
在一点的导数值为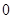 是函数
是函数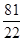
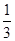
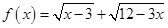 的最大值为M,最小值为m,则
的最大值为M,最小值为m,则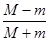 的值为( )
的值为( )


