题目内容
已知函数 的导函数存在,则函数
的导函数存在,则函数 在一点的导数值为
在一点的导数值为 是函数
是函数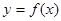 在这点取极值的( )
在这点取极值的( )
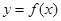 的导函数存在,则函数
的导函数存在,则函数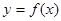 在一点的导数值为
在一点的导数值为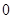 是函数
是函数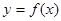 在这点取极值的( )
在这点取极值的( )| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
B
试题分析:因为函数
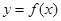 的导函数存在,所以当函数
的导函数存在,所以当函数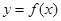 在
在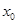 处取得极值时,必有
处取得极值时,必有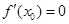 ;反过来若
;反过来若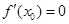 ,函数
,函数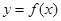 在
在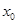 处不一定取得极值,如
处不一定取得极值,如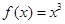 ,
,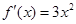 ,有
,有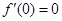 ,但由于
,但由于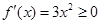 恒成立,所以
恒成立,所以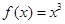 在
在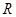 上单调递增,
上单调递增,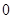 并不是函数
并不是函数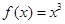 的极值点,故选B.
的极值点,故选B.
练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
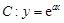 .
.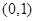 处的切线为
处的切线为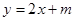 ,求实数
,求实数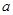 和
和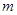 的值;
的值;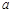 ,曲线
,曲线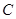 总在直线
总在直线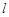 :
: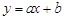 的上方,求实数
的上方,求实数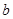 的取值范围.
的取值范围. ,
,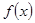 的极值点;
的极值点;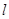 过点
过点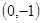 ,并且与曲线
,并且与曲线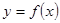 相切,求直线
相切,求直线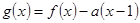 ,其中
,其中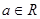 ,求函数
,求函数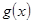 在
在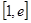 上的最小值(其中
上的最小值(其中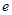 为自然对数的底数).
为自然对数的底数).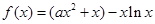 在
在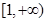 上单调递增,则实数
上单调递增,则实数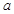 的取值范围是 ;
的取值范围是 ;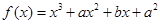 .在
.在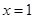 处有极值10,则
处有极值10,则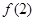 等于_______.
等于_______.