题目内容
14.已知函数f(x)=$\frac{1}{3}{x^3}$-4x+4(1)求函数的极值;
(2)若函数f(x)=k有3个解,求实数k的取值范围.
分析 (1)先求出函数的导数,得到函数的单调区间,从而求出函数的极值;(2)画出函数f(x)的图象,结合图象从而求出k的范围.
解答 解:(1)f′(x)=x2-4=(x+2)(x-2),
令f′(x)=0,解得:x=2或x=-2,
当x变化时,f′(x)、f(x)的变化情况如下表:
| x | (-∞,-2) | -2 | (-2,2) | 2 | (2,+∞) |
| f′(x) | + | 0 | - | 0 | + |
| f(x) | 单调递增↗ | $\frac{28}{3}$ | 单调递减↘ | $-\frac{4}{3}$ | 单调递增↗ |
当x=2时,f(x)有极小值$-\frac{4}{3}$;
(2)函数$f(x)=\frac{1}{3}{x^3}-4x+4$的图象,大致如图:
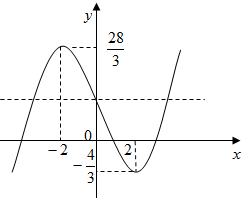
若函数f(x)=k有3个解,
即函数y=k和y=f(x)的图象有3个交点,
由图可知:$-\frac{4}{3}<k<\frac{28}{3}$.
点评 本题考查了函数的单调性,函数的极值问题,考查导数的应用,数形结合思想,是一道中档题.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案
相关题目
6.已知$\overrightarrow{{e}_{1}}$,$\overrightarrow{{e}_{2}}$是互相垂直的两个单位向量,若$\overrightarrow{a}$=2$\overrightarrow{{e}_{1}}$-$\overrightarrow{{e}_{2}}$,则|$\overrightarrow{a}$|等于( )
| A. | 1 | B. | $\sqrt{5}$ | C. | 3 | D. | 5 |
7.已知等比数列{an}公比为q,其前n项和为Sn,若S3、S9、S6成等差数列,则q3等于( )
| A. | -$\frac{1}{2}$ | B. | 1 | C. | -$\frac{1}{2}$或1 | D. | -1或$\frac{1}{2}$ |
9.已知点A(1,-1)及圆x2+y2-4x+4y=0,则过点A,且在圆上截得的弦最长的直线方程是( )
| A. | x-1=0 | B. | x+y=0 | C. | y+1=0 | D. | x-y-2=0 |
19.设数列{an}是首项为1的等比数列,若{$\frac{1}{2{a}_{n}+{a}_{n+1}}$}是等差数列,则($\frac{1}{2{a}_{1}}$+$\frac{1}{{a}_{2}}$)+($\frac{1}{2{a}_{2}}$+$\frac{1}{{a}_{3}}$)+…($\frac{1}{2{a}_{2014}}$+$\frac{1}{{a}_{2015}}$)的值等于( )
| A. | 2014 | B. | 2015 | C. | 3020 | D. | 3021 |
3.集合P={x,1},Q={0,1,2},P∩Q={0,1},则x为( )
| A. | 0 | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |
4.若(m-1)+(3m+2)i是纯虚数,则实数m的值为( )
| A. | 1 | B. | 1或2 | C. | 0 | D. | -1、1、2 |