题目内容
6．已知$\overrightarrow{{e}_{1}}$，$\overrightarrow{{e}_{2}}$是互相垂直的两个单位向量，若$\overrightarrow{a}$=2$\overrightarrow{{e}_{1}}$-$\overrightarrow{{e}_{2}}$，则|$\overrightarrow{a}$|等于（ ）| A． | 1 | B． | $\sqrt{5}$ | C． | 3 | D． | 5 |
分析 由题意，先求|$\overrightarrow{a}$|2，然后开方求模．
解答 解：因为$\overrightarrow{{e}_{1}}$，$\overrightarrow{{e}_{2}}$是互相垂直的两个单位向量，所以$\overrightarrow{{e}_{1}}•\overrightarrow{{e}_{2}}$=0，又$\overrightarrow{a}$=2$\overrightarrow{{e}_{1}}$-$\overrightarrow{{e}_{2}}$，则|$\overrightarrow{a}$|2=$4{\overrightarrow{{e}_{1}}}^{2}-4\overrightarrow{{e}_{1}}•\overrightarrow{{e}_{2}}+{\overrightarrow{{e}_{2}}}^{2}$=4-0+1=5；所以|$\overrightarrow{a}$|=$\sqrt{5}$；
故选：B．
点评 本题考查了平面向量模的求法；解答本题的关键是利用$\overrightarrow{{e}_{1}}$，$\overrightarrow{{e}_{2}}$的模及数量积表示|$\overrightarrow{a}$|2．
练习册系列答案
相关题目
16．函数f（x）=$\frac{sinx}{x}$的导数是（ ）
| A． | $\frac{xsinx+cosx}{{x}^{2}}$ | B． | $\frac{xcosx+sinx}{{x}^{2}}$ | C． | $\frac{xcosx-sinx}{{x}^{2}}$ | D． | $\frac{xsinx-cosx}{{x}^{2}}$ |
17．
从某企业生茶的某种产品中抽取100件，测量这些产品的一项质量指标值，由测量结果得如下频数分布表：
（1）在答题卡上补全这些数据作出的频率分布直方图；
（2）估计这种产品质量指标值的平均值及方差（同一组中的数据用该组区间的中点值作代表）；
（3）估计这种产品质量指标值的中位数．（精确到0.1）
从某企业生茶的某种产品中抽取100件，测量这些产品的一项质量指标值，由测量结果得如下频数分布表：| 质量指标值分组 | [75，85） | [85，95） | [95，105） | [105，115） | [115，125） |
| 频数 | 6 | 28 | 34 | 24 | 8 |
（2）估计这种产品质量指标值的平均值及方差（同一组中的数据用该组区间的中点值作代表）；
（3）估计这种产品质量指标值的中位数．（精确到0.1）
14．如图表示的是求首项为-41，公差为2的等差数列{an}前n项和的最小值的程序框图．则①处可填写（ ）
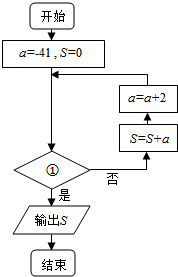
| A． | S＞0 | B． | S＜0 | C． | a＞0 | D． | a=0 |
15．已知函数f（x）=ex-e-x（e=2.71828…）是自然对数的底数），f（x）的导数是（ ）
| A． | 偶函数 | B． | 奇函数 | C． | 增函数 | D． | 减函数 |