题目内容
对抛物线x2=-4y,下列描述正确的是( )
A.开口向下,焦点为(0,-
| ||
| B.开口向下,焦点为(0,-1) | ||
C.开口向左,焦点为(-
| ||
| D.开口向左,焦点为(-1,0) |
∵抛物线方程为x2=-4y,∴由x2=-4y≥0,得y≤0.
即抛物线上点的纵坐标为负数或零,因此抛物线分布在三四象限,可得它的开口向下;
又∵2p=4,得
=1,∴抛物线的焦点坐标为(0,-1).
综上所述,抛物线x2=-4y开口向下且焦点为(0,-1).
故选:B
即抛物线上点的纵坐标为负数或零,因此抛物线分布在三四象限,可得它的开口向下;
又∵2p=4,得
| p |
| 2 |
综上所述,抛物线x2=-4y开口向下且焦点为(0,-1).
故选:B

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
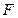 和定直线
和定直线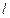 ,动圆
,动圆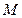 过
过