题目内容
设圆C的圆心在双曲线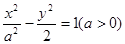 的右焦点且与此双曲线的渐近线相切,若圆C被直线
的右焦点且与此双曲线的渐近线相切,若圆C被直线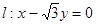 截得的弦长等于2,则a的值为 ( )
截得的弦长等于2,则a的值为 ( )
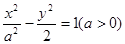 的右焦点且与此双曲线的渐近线相切,若圆C被直线
的右焦点且与此双曲线的渐近线相切,若圆C被直线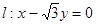 截得的弦长等于2,则a的值为 ( )
截得的弦长等于2,则a的值为 ( )A.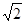 | B.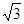 | C.2 | D.3 |
A
分析:圆C的圆心C(
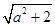 ,0),双曲线的渐近线方程为
,0),双曲线的渐近线方程为  x±ay=0,再由C到渐近线的距离可求出圆C方程(x-
x±ay=0,再由C到渐近线的距离可求出圆C方程(x- 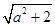 )2+y2=2.由l被圆C截得的弦长是2及圆C的半径为
)2+y2=2.由l被圆C截得的弦长是2及圆C的半径为  可知
可知 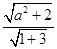 =1,由此能求出a的值.
=1,由此能求出a的值.解:圆C的圆心C(
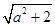 ,0),
,0),双曲线的渐近线方程为
 x±ay=0,
x±ay=0,C到渐近线的距离为d=
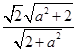 =
= ,
,故圆C方程(x-
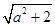 )2+y2=2.
)2+y2=2.由l被圆C截得的弦长是2及圆C的半径为
 可知,
可知,圆心C到直线l的距离为1,
即
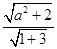 =1,
=1,∴a=
 .
.故选A.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
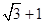 B.
B.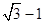
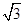 D.
D.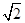
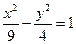 中的被点
中的被点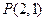 平分的弦所在的直线方程是( ).
平分的弦所在的直线方程是( ).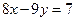
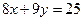
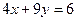
 是双曲线
是双曲线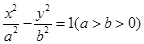
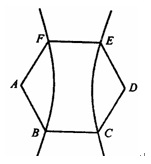
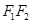 为边作正三角形
为边作正三角形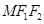 ,若边
,若边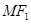 的中点在双曲线上,则双曲线的离心率是( )
的中点在双曲线上,则双曲线的离心率是( )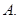
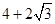
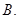
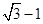
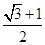
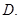
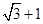
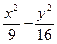 ="1"
="1"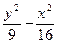 =1
=1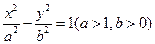 的焦距为
的焦距为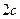 ,离心率为
,离心率为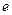 ,若点
,若点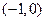 与
与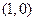 到直线
到直线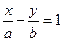 的距离之和
的距离之和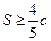 ,则
,则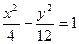 上一点P到它的右焦点的距离是8,那么点P到它的左焦点的距离是( )
上一点P到它的右焦点的距离是8,那么点P到它的左焦点的距离是( )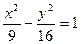 有共同的渐近线,并且过点A(
有共同的渐近线,并且过点A(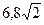 )的双曲线的标准方程为________________________.
)的双曲线的标准方程为________________________.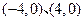 ,则双曲线的方程为
,则双曲线的方程为