题目内容
正四面体的四个顶点都在表面积为36π的一个球面上，求这个四面体的高.
解析：设球的半径为R，则S球=4πR2.∴4πR2=36π 
R=3.如图，
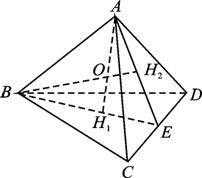
正四面体A—BCD，H1、H2分别是A、B在底面BCD和底面ACD的射影，AH1与BH2交于O，AH2与BH1交于E，则E为CD的中点，O为球心，H1、H2分别为△BCD和△ACD的中心.显然OA=R=3.
令AB=a，则AE=
a，AH2=
AE=
a,H2E=H1E= 
AE=
a,
∴AH1=
a.
显然△AH2O∽△AH1E，∴OA·AH1=AH2·AE.
∴3·
a=
a·
a.
∴a=2
.∴AH1=
×2
=4.
∴四面体的高为4.
练习册系列答案
相关题目
棱长为2的正四面体的四个顶点都在同一个球面上，若过该球球心的一个截面如图，则图中三角形（正四面体的截面）的面积是（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
