题目内容
正四面体的四个顶点都在一个球面上，且正四面体的高为4，则球的表面积为（ ）
分析：如图所示：设正四面体的棱长等于a，球的半径等于r，先求出BH的值，用勾股定理求出AH，再由AH=4求出a的值，Rt△BOH中，由勾股定理求得r的值，代入球的表面积公式求出球的表面积．
解答：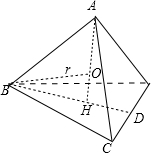
解：如图所示：设正四面体的棱长等于a，球的半径等于r，作AH垂直于平面BCD，H为垂足．
则BH=
•BD=
•
a=
a，故AH=
=
=
a．
再由AH=4，可得
a=4，∴a=
．
Rt△BOH中，由勾股定理可得 r2= (4-r)2+(
a)2，解得r=3．
故球的表面积为4πr2=36π，
故选C．
解：如图所示：设正四面体的棱长等于a，球的半径等于r，作AH垂直于平面BCD，H为垂足．则BH=
| 2 |
| 3 |
| 2 |
| 3 |
| ||
| 2 |
| ||
| 3 |
| AB2-BH2 |
a2-(
|
| ||
| 3 |
再由AH=4，可得
| ||
| 3 |
| 12 | ||
|
Rt△BOH中，由勾股定理可得 r2= (4-r)2+(
| ||
| 3 |
故球的表面积为4πr2=36π，
故选C．
点评：本题主要考查球的内接正四面体的性质，求球的表面积的方法，体现了数形结合的数学思想．
练习册系列答案
相关题目
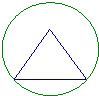棱长为2的正四面体的四个顶点都在同一个球面上，若过该球球心的一个截面如图，则图中三角形（正四面体的截面）的面积是（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
