Question

棱长为2的正四面体的四个顶点都在同一个球面上，若过该球球心的一个截面如图，则图中三角形（正四面体的截面）的面积是（　　）

• A、

  2

  2

• B、

  3

  2

• C、

  2

• D、

  3

Answer 1

分析：做本题时，需要将原图形在心中还原出来，最好可以做出图形，利用图形关系，就可以求解了．

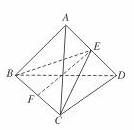
解答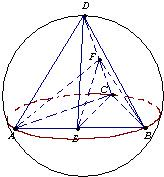：解：棱长为2的正四面体ABCD的四个顶点都在同一个球面上，若过该球球心的一个截面如图为△ABF，则图中AB=2，E为AB中点，则EF⊥DC，
在△DCE中，DE=EC=

3

，DC=2，
∴EF=

2

，
∴三角形ABF的面积是

2

，
故选C．

点评：本题考查学生的空间想象能力，以及学生对几何体的认识，是中档题．