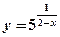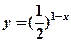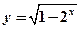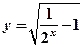题目内容
(3分)已知
(1)判断f(x)的单调性;
(2)设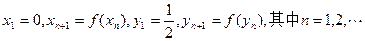
证明: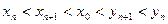
(3)证明: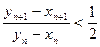

(1)判断f(x)的单调性;
(2)设
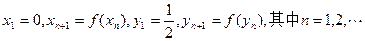
证明:
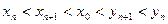
(3)证明:
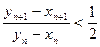
f(x)在R上是单调递增函数
(1)∵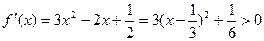
∴f(x)在R上是单调递增函数…………(3分)
(2)∵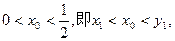 又f(x)是R上的增函数
又f(x)是R上的增函数
∴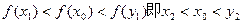
又∵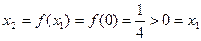
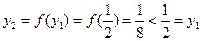
综合上述: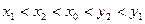 ………………(6分)
………………(6分)
用数学归纳法证明如下:
①当n=1时,上面已证成立
②假设当n=k(k≥1)时有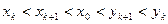 成立
成立
当n=k+1时,由f(x)在R上单调递增
∴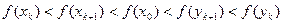
∴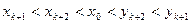
由①②对一切n∈N*,都有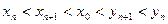 …………(9分)
…………(9分)
(3)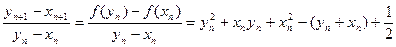
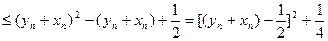
由(2)知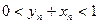
∴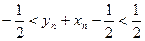
∴ …………(13分)
…………(13分)
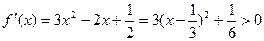
∴f(x)在R上是单调递增函数…………(3分)
(2)∵
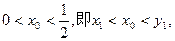 又f(x)是R上的增函数
又f(x)是R上的增函数∴
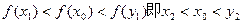
又∵
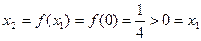
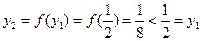
综合上述:
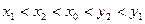 ………………(6分)
………………(6分)用数学归纳法证明如下:
①当n=1时,上面已证成立
②假设当n=k(k≥1)时有
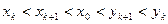 成立
成立当n=k+1时,由f(x)在R上单调递增
∴
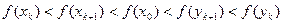
∴
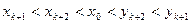
由①②对一切n∈N*,都有
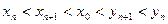 …………(9分)
…………(9分)(3)
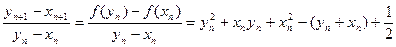
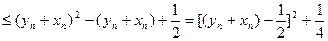
由(2)知
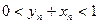
∴
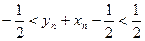
∴
 …………(13分)
…………(13分)
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
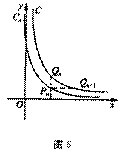
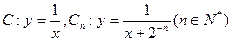 。从C上的点Qn(
。从C上的点Qn( )作x轴的垂线,交
)作x轴的垂线,交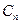 于点
于点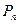 ,再从
,再从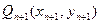 。设
。设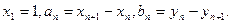
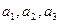 的值,由此猜想数列
的值,由此猜想数列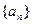 的通项公式(不用证明);
的通项公式(不用证明);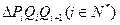 和面积为
和面积为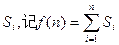 ,求证
,求证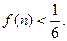
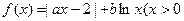 ,实数a,b为常数),
,实数a,b为常数), 在(0,+∞)上是单调增函数,求b的取值范围;
在(0,+∞)上是单调增函数,求b的取值范围;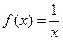 在(0,1]上解的个数。
在(0,1]上解的个数。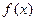 的定义域为
的定义域为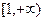 ,且
,且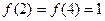 ,
,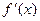 为
为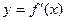 的图象如图所示,则不等式组
的图象如图所示,则不等式组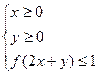 所表示的平面区域的面积是( )
所表示的平面区域的面积是( )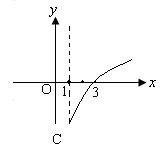
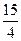

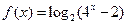 ,则方程
,则方程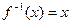 的解为 .
的解为 .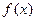 在
在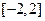 内的图象如图所示,若函数
内的图象如图所示,若函数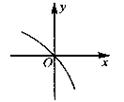
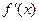 的图象也是连续不间断的,
的图象也是连续不间断的,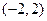 内有零点( )
内有零点( )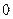 个
个 个
个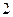 个
个 个
个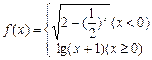 ,若
,若 ,则
,则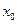 的取值范围是 ( )
的取值范围是 ( )
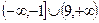
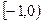
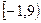
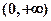 的函数是
的函数是