题目内容
(本题14分)
已知函数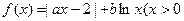 ,实数a,b为常数),
,实数a,b为常数),
(1)若a=1, 在(0,+∞)上是单调增函数,求b的取值范围;
在(0,+∞)上是单调增函数,求b的取值范围;
(2)若a≥2,b=1,求方程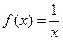 在(0,1]上解的个数。
在(0,1]上解的个数。
已知函数
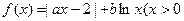 ,实数a,b为常数),
,实数a,b为常数),(1)若a=1,
 在(0,+∞)上是单调增函数,求b的取值范围;
在(0,+∞)上是单调增函数,求b的取值范围;(2)若a≥2,b=1,求方程
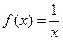 在(0,1]上解的个数。
在(0,1]上解的个数。(1)b≥2
(2)解的个数为0个
(2)解的个数为0个
(1)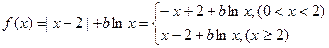
①当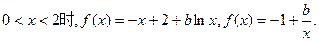
由条件,得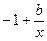 ≥0恒成立,即b≥x恒成立。
≥0恒成立,即b≥x恒成立。
∴b≥2
②当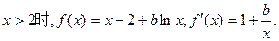
 由条件,得
由条件,得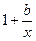 ≥0恒成立,即b≥-x恒成立
≥0恒成立,即b≥-x恒成立
∴b≥-2
∵f (x)的图象在(0,+∞)不间断,
综合①,②得b的取值范围是b≥2。
(2)令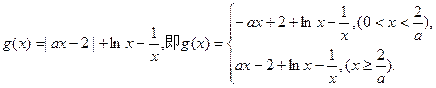
当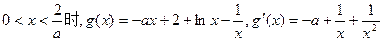 ,
,
∵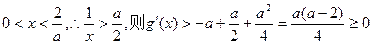
即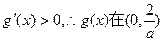 上是单调增函数。
上是单调增函数。
当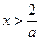 时,
时,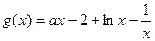 ,
,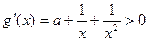
∴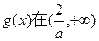 上是单调增函数。
上是单调增函数。
∵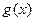 的图象在
的图象在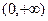 上不间断,∴
上不间断,∴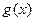 在
在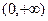 上是单调增函数。
上是单调增函数。
∵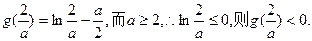
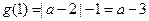

①当a≥3时,∵g (1) ≥0,∴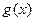 =0在(0,1]上有惟一解。
=0在(0,1]上有惟一解。
即方程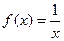 解的个数为1个。
解的个数为1个。
②当2≤a<3时,∵g (1) <0,∴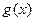 =0在(0,1]上无解。
=0在(0,1]上无解。
即方程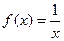 解的个数为0个。
解的个数为0个。
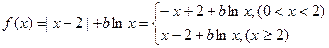
①当
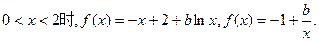
由条件,得
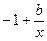 ≥0恒成立,即b≥x恒成立。
≥0恒成立,即b≥x恒成立。∴b≥2
②当
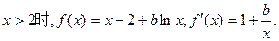
 由条件,得
由条件,得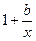 ≥0恒成立,即b≥-x恒成立
≥0恒成立,即b≥-x恒成立∴b≥-2
∵f (x)的图象在(0,+∞)不间断,
综合①,②得b的取值范围是b≥2。
(2)令
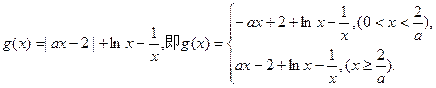
当
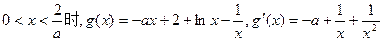 ,
,∵
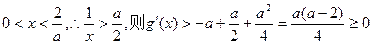
即
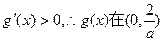 上是单调增函数。
上是单调增函数。当
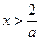 时,
时,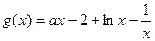 ,
,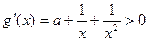
∴
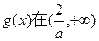 上是单调增函数。
上是单调增函数。∵
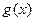 的图象在
的图象在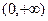 上不间断,∴
上不间断,∴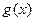 在
在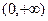 上是单调增函数。
上是单调增函数。∵
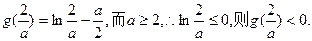
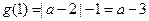

①当a≥3时,∵g (1) ≥0,∴
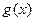 =0在(0,1]上有惟一解。
=0在(0,1]上有惟一解。即方程
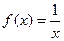 解的个数为1个。
解的个数为1个。②当2≤a<3时,∵g (1) <0,∴
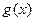 =0在(0,1]上无解。
=0在(0,1]上无解。即方程
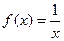 解的个数为0个。
解的个数为0个。
练习册系列答案
相关题目
 一辆.
一辆. 租出的车每辆每月需维护费150元,未租出的车每辆每月需维护费50元.
租出的车每辆每月需维护费150元,未租出的车每辆每月需维护费50元.
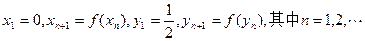
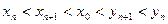
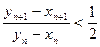
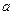 人,每人每年可创纯利润1万元.据评估,在生产条件不变的条件下,每裁员一人,则留岗员工每人每年可多创收0.01万元,但每年需付给下岗工人0.4万元生活费,并且企业正常运行所需人数不得少于现有员工的
人,每人每年可创纯利润1万元.据评估,在生产条件不变的条件下,每裁员一人,则留岗员工每人每年可多创收0.01万元,但每年需付给下岗工人0.4万元生活费,并且企业正常运行所需人数不得少于现有员工的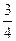 ,设该企业裁员
,设该企业裁员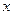 人后纯收益为
人后纯收益为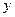 万元.
万元.
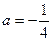 ”是“函数
”是“函数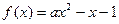 只有一个零点”的( )
只有一个零点”的( )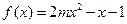 在区间
在区间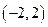 恰有一个零点,则
恰有一个零点,则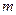 的取值范围是( )
的取值范围是( )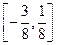
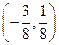
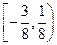
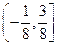
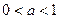 ,则方程
,则方程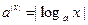 的实根个数为
的实根个数为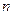 ,且
,且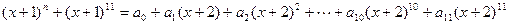 ,则
,则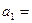 ( )
( )