题目内容
某校开设A类选修课3门,B类选修课4门,一位同学从中共选3门,若要求两类课程中各至少选一门,则不同的选法共有 种(用数字作答).
30
解析考点:组合及组合数公式。
分析:由题意分类:(1)A类选修课选1门,B类选修课选2门,确定选法;(2)A类选修课选2门,B类选修课选1门,确定选法;然后求和即可。
解答:
分以下2种情况:
(1)A类选修课选1门,B类选修课选2门,有C31C42种不同的选法;
(2)A类选修课选2门,B类选修课选1门,有C32C41种不同的选法。
所以不同的选法共有C31C42+C32C41=18+12=30种。
故答案为:30。
点评:本小题主要考查分类计数原理、组合知识,以及分类讨论的数学思想。

练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案
相关题目
 的展开式中,含
的展开式中,含 的项的系数是
的项的系数是 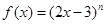 展开式的二项式系数和为512,且
展开式的二项式系数和为512,且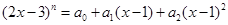
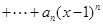 .
.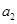 的值; (2)求
的值; (2)求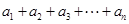 的值.
的值. )7展开式中x3的系数为 .
)7展开式中x3的系数为 .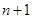 个球(其中
个球(其中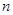 个白球,1个黑球)的口袋中取出
个白球,1个黑球)的口袋中取出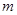 个球
个球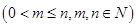 ,共有
,共有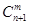 种取法,这
种取法,这 种取法,另一类是取出的
种取法,另一类是取出的 种取法,由此可得等式:
种取法,由此可得等式: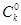 ·
·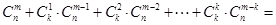 .
.  的展开式中的常数项是_____________.
的展开式中的常数项是_____________.