题目内容
设函数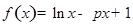 .
.
(1)研究函数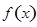 的极值点;
的极值点;
(2)当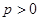 时,若对任意的
时,若对任意的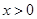 ,恒有
,恒有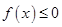 ,求
,求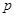 的取值范围;
的取值范围;
(3)证明: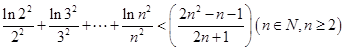 .
.
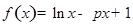 .
.(1)研究函数
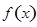 的极值点;
的极值点;(2)当
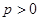 时,若对任意的
时,若对任意的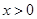 ,恒有
,恒有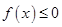 ,求
,求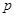 的取值范围;
的取值范围;(3)证明:
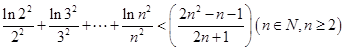 .
.(1)详见解析;(2)实数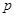 的取值范围是
的取值范围是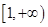 ;(3)详见解析.
;(3)详见解析.
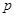 的取值范围是
的取值范围是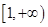 ;(3)详见解析.
;(3)详见解析.试题分析:(1)先求出函数
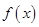 的导数
的导数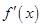 ,对
,对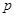 的符号进行分类讨论,即对函数
的符号进行分类讨论,即对函数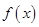 是否存在极值点进行分类讨论,结合函数的单调性或导数符号确定函数的极大值或极小值;(2)利用(1)中的结论,将问题转化为
是否存在极值点进行分类讨论,结合函数的单调性或导数符号确定函数的极大值或极小值;(2)利用(1)中的结论,将问题转化为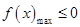 ,结合(1)中的结论列不等式解参数
,结合(1)中的结论列不等式解参数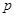 的取值范围;(3)在(2)中,令
的取值范围;(3)在(2)中,令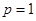 ,得到不等式
,得到不等式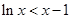 在
在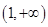 上恒成立,然后令
上恒成立,然后令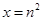 得到
得到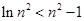 ,两边同除以
,两边同除以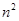 得到
得到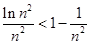 ,结合放缩法得到
,结合放缩法得到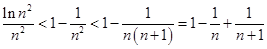 ,最后;利用累加法即可得到所证明的不等式.
,最后;利用累加法即可得到所证明的不等式.试题解析:(1)
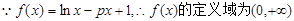 ,
,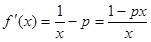
当
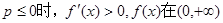 上无极值点
上无极值点 当p>0时,令
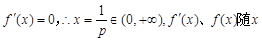 的变化情况如下表:
的变化情况如下表:| x | (0,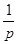 ) ) | 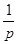 | 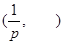 |
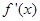 | + | 0 | - |
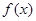 | ↗ | 极大值 | ↘ |
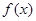 有唯一的极大值点
有唯一的极大值点
(2)当
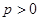 时在
时在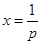 处取得极大值
处取得极大值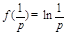 ,
,此极大值也是最大值,要使
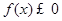 恒成立,只需
恒成立,只需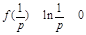 ,
,∴
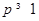 ,即p的取值范围为[1,+∞
,即p的取值范围为[1,+∞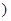 ;
;(3)令
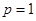 ,由(2)知,
,由(2)知,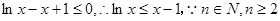
∴
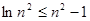 ,∴
,∴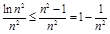 ,
,∴
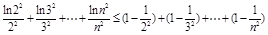
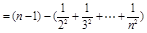
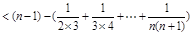
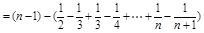
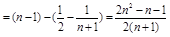 ,∴结论成立
,∴结论成立 另解:设函数
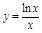 ,则
,则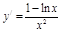 ,令
,令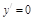 ,解得
,解得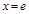 ,则
,则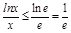 ,
,∴
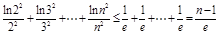 =
=
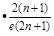 =
= (
(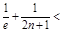


练习册系列答案
 金钥匙试卷系列答案
金钥匙试卷系列答案
相关题目
 在
在 上是增函数,
上是增函数, 上是减函数.
上是减函数. 的解析式;
的解析式; 时,
时, 恒成立,求实数m的取值范围;
恒成立,求实数m的取值范围; 在区间
在区间 上恰有两个相异实数根,若存在,求出b的范围,若不存在说明理由.
上恰有两个相异实数根,若存在,求出b的范围,若不存在说明理由.

 时,求
时,求 的单调区间;
的单调区间; ,设
,设 是函数
是函数 ,记
,记 分别为
分别为 ,求实数
,求实数 的取值范围.
的取值范围.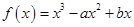 的图象与直线
的图象与直线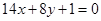 相切于点
相切于点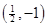 .
.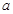 和
和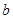 的值; (2)求
的值; (2)求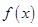 的极值.
的极值.

 时,求函数
时,求函数 的极大值和极小值;
的极大值和极小值; 时,
时, 恒成立,求
恒成立,求 的取值范围.
的取值范围.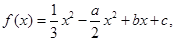 其中
其中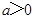 ,曲线
,曲线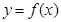 在点
在点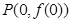 处的切线方程为
处的切线方程为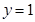 .
.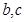 的值;
的值;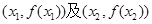 处的切线都过点(0,2).证明:当
处的切线都过点(0,2).证明:当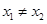 时,
时,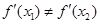 ;
;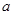 的取值范围.
的取值范围.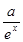 ,x
,x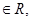 已知斜率为k的直线与y=f(x)的图象交于A(x1,y1),B(x2,y2)(x1
已知斜率为k的直线与y=f(x)的图象交于A(x1,y1),B(x2,y2)(x1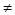 x2)两点,若对任意的a<一2,k>m恒成立,则m的最大值为( )
x2)两点,若对任意的a<一2,k>m恒成立,则m的最大值为( )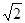
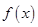 在R上可导,函数
在R上可导,函数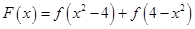 ,则
,则 .
. 的图象在点
的图象在点 处的切线方程为
处的切线方程为 ,则函数
,则函数 的图象在点
的图象在点 处的切线方程为 .
处的切线方程为 .