题目内容
若点 的坐标为
的坐标为 ,
, 是抛物线
是抛物线 的焦点,点
的焦点,点 在抛物线上移动时,使
在抛物线上移动时,使 取得最小值的
取得最小值的 的坐标为( )
的坐标为( )
A. | B. | C. | D. |
D
解析试题分析:求出焦点坐标和准线方程,把|MF|+|MA|转化为|MA|+|PM|,利用 当P、A、M三点共线时,|MA|+|PM|取得最小值,把y=2代入抛物线y2="2x" 解得x值,即得M的坐标.解:由题意得 F( ,0),准线方程为 x=-
,0),准线方程为 x=- ,设点M到准线的距离为d=|PM|,则由抛物线的定义得|MA|+|MF|=|MA|+|PM|,故当P、A、M三点共线时,|MF|+|MA|取得最小值为|AP|=3-(-
,设点M到准线的距离为d=|PM|,则由抛物线的定义得|MA|+|MF|=|MA|+|PM|,故当P、A、M三点共线时,|MF|+|MA|取得最小值为|AP|=3-(- )=
)= .把 y=2代入抛物线y2="2x" 得 x=2,故点M的坐标是(2,2),故选D.
.把 y=2代入抛物线y2="2x" 得 x=2,故点M的坐标是(2,2),故选D.
考点:抛物线的定义和性质
点评:本题考查抛物线的定义和性质得应用,解答的关键利用是抛物线定义,体现了转化的数学思想

练习册系列答案
相关题目
如果椭圆 上一点P到焦点F1的距离为6,则点P到另一个焦点F2的距离为( )
上一点P到焦点F1的距离为6,则点P到另一个焦点F2的距离为( )
| A.10 | B.6 | C.12 | D.14 |
过双曲线 的左焦点
的左焦点 作圆
作圆 的切线交双曲线右支于点
的切线交双曲线右支于点 ,切点为
,切点为 ,若
,若 ,则双曲线的离心率为
,则双曲线的离心率为
A. | B. | C. | D. |
已知椭圆 与曲线
与曲线 的离心率互为倒数,则
的离心率互为倒数,则 ( )
( )
| A.16 | B. | C. | D. |

 的右焦点为
的右焦点为 ,过点
,过点 轴垂直的直线
轴垂直的直线 交两渐近线于A,B两点,与双曲线的其中一个交点为
交两渐近线于A,B两点,与双曲线的其中一个交点为 ,设O为坐标原点,若
,设O为坐标原点,若 (
( ),且
),且 ,则该双曲线的离心率为
,则该双曲线的离心率为



 ,曲线C2:
,曲线C2: ,EF是曲线C1的任意一条直径,P是曲线C2上任一点,则
,EF是曲线C1的任意一条直径,P是曲线C2上任一点,则 ·
· 的最小值为 ( )
的最小值为 ( )
 与双曲线
与双曲线 相交于ABCD四点,若四边形ABCD是正方形,则双曲线的离心率的取值范围为( )
相交于ABCD四点,若四边形ABCD是正方形,则双曲线的离心率的取值范围为( )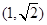



 是双曲线
是双曲线 的左、右焦点,过
的左、右焦点,过 且垂直于
且垂直于 轴的直线与双曲线交于
轴的直线与双曲线交于 两点,若△
两点,若△ 是锐角三角形,则该双曲线离心率的取值范围是( )
是锐角三角形,则该双曲线离心率的取值范围是( )



 ; ②y=2; ③
; ②y=2; ③ ; ④
; ④ .
.