题目内容
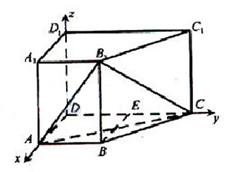
如图,在四棱柱 中,侧棱
中,侧棱 底面
底面 ,
,

(Ⅰ)求证: 平面
平面
(Ⅱ)若直线 与平面
与平面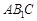 所成角的正弦值为
所成角的正弦值为 ,求
,求 的值
的值
(Ⅲ)现将与四棱柱 形状和大小完全相同的两个四棱柱拼成一个新的四棱柱,规定:若拼成的新四棱柱形状和大小完全相同,则视为同一种拼接方案,问共有几种不同的拼接方案?在这些拼接成的新四棱柱中,记其中最小的表面积为
形状和大小完全相同的两个四棱柱拼成一个新的四棱柱,规定:若拼成的新四棱柱形状和大小完全相同,则视为同一种拼接方案,问共有几种不同的拼接方案?在这些拼接成的新四棱柱中,记其中最小的表面积为 ,写出
,写出 的解析式。(直接写出答案,不必说明理由)
的解析式。(直接写出答案,不必说明理由)
 中,侧棱
中,侧棱 底面
底面 ,
,

(Ⅰ)求证:
 平面
平面
(Ⅱ)若直线
 与平面
与平面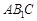 所成角的正弦值为
所成角的正弦值为 ,求
,求 的值
的值(Ⅲ)现将与四棱柱
 形状和大小完全相同的两个四棱柱拼成一个新的四棱柱,规定:若拼成的新四棱柱形状和大小完全相同,则视为同一种拼接方案,问共有几种不同的拼接方案?在这些拼接成的新四棱柱中,记其中最小的表面积为
形状和大小完全相同的两个四棱柱拼成一个新的四棱柱,规定:若拼成的新四棱柱形状和大小完全相同,则视为同一种拼接方案,问共有几种不同的拼接方案?在这些拼接成的新四棱柱中,记其中最小的表面积为 ,写出
,写出 的解析式。(直接写出答案,不必说明理由)
的解析式。(直接写出答案,不必说明理由)(Ⅰ)见解析(Ⅱ)1(Ⅲ)共有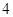 种不同的方案
种不同的方案
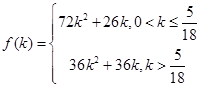
 种不同的方案
种不同的方案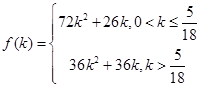
(Ⅰ)取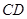 中点
中点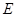 ,连接
,连接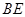
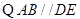 ,
,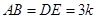
 四边形
四边形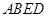 为平行四边形
为平行四边形
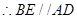 且
且
在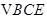 中,
中,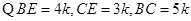
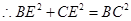
 ,即
,即 ,又
,又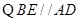 ,所以
,所以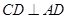
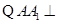 平面
平面 ,
,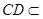 平面
平面
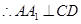 ,又
,又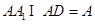 ,
,
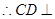 平面
平面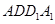
(Ⅱ)以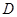 为原点,
为原点, 的方向为
的方向为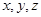 轴的正方向建立如图所示的空间直角坐标系
轴的正方向建立如图所示的空间直角坐标系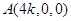 ,
, ,
, ,
,
所以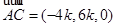 ,
, ,
,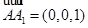
设平面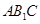 的法向量
的法向量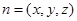 ,则由
,则由
得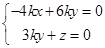 取
取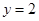 ,得
,得
设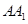 与平面
与平面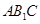 所成角为
所成角为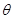 ,则
,则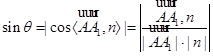
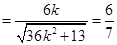 ,解得
,解得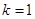 .故所求
.故所求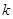 的值为1
的值为1
(Ⅲ)共有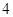 种不同的方案
种不同的方案
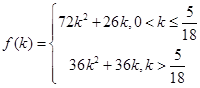
立体几何第一问对于关系的决断往往基于对公理定理推论掌握的比较熟练,又要善于做出一线辅助线加以证明,那么第二问就可以在其基础上采用坐标法处理角度或者距离问题,坐标法所用的公式就必需熟练掌握,第三问主要考查了学生的空间思维能力,要在平时多加练习。此题坐标法也很考验学生的计算功底。
【考点定位】 本题主要考查立体几何中线线关系线面关系的判断以及线面角的算法,并且通过第三问的设问又把几何体的表面积与函数巧妙的结合起来,计算和空间思维要求比较高。属于难题。
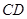 中点
中点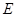 ,连接
,连接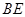

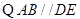 ,
,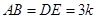
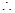 四边形
四边形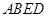 为平行四边形
为平行四边形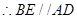 且
且
在
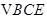 中,
中,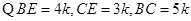
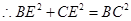
 ,即
,即 ,又
,又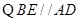 ,所以
,所以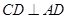
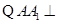 平面
平面 ,
,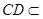 平面
平面
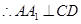 ,又
,又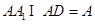 ,
,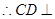 平面
平面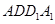
(Ⅱ)以
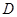 为原点,
为原点, 的方向为
的方向为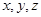 轴的正方向建立如图所示的空间直角坐标系
轴的正方向建立如图所示的空间直角坐标系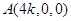 ,
, ,
, ,
,
所以
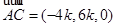 ,
, ,
,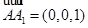
设平面
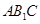 的法向量
的法向量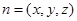 ,则由
,则由
得
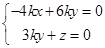 取
取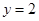 ,得
,得
设
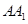 与平面
与平面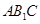 所成角为
所成角为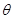 ,则
,则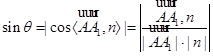
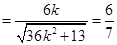 ,解得
,解得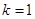 .故所求
.故所求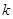 的值为1
的值为1(Ⅲ)共有
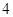 种不同的方案
种不同的方案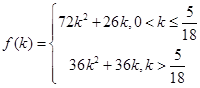
立体几何第一问对于关系的决断往往基于对公理定理推论掌握的比较熟练,又要善于做出一线辅助线加以证明,那么第二问就可以在其基础上采用坐标法处理角度或者距离问题,坐标法所用的公式就必需熟练掌握,第三问主要考查了学生的空间思维能力,要在平时多加练习。此题坐标法也很考验学生的计算功底。
【考点定位】 本题主要考查立体几何中线线关系线面关系的判断以及线面角的算法,并且通过第三问的设问又把几何体的表面积与函数巧妙的结合起来,计算和空间思维要求比较高。属于难题。

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
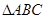 是边长为2的正三角形. 若
是边长为2的正三角形. 若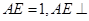 平面
平面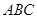 ,平面
,平面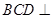 平面
平面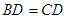 ,且
,且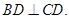
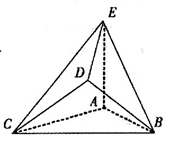
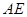 //平面
//平面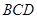 ;
; 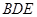
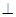 平面
平面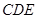 .
. 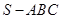 中,平面
中,平面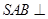 平面
平面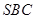 ,
,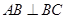 ,
,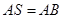 . 过点
. 过点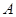 作
作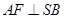 ,垂足为
,垂足为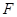 ,点
,点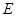 ,
,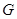 分别为棱
分别为棱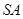 ,
,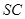 的中点.
的中点.
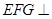 平面
平面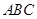 ;
;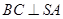 .
.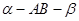 与
与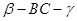 均为
均为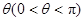 ,
,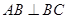 ,
,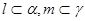 ,则下列不可能成立的是( )
,则下列不可能成立的是( )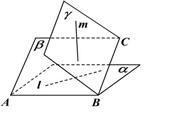




 是不同的平面,下列命题中正确的是
是不同的平面,下列命题中正确的是



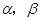 ,直线
,直线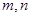 ,下列命题中不正确的是 ( )
,下列命题中不正确的是 ( )



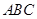 中,
中,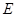 、
、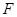 、
、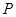 分别是
分别是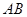 、
、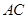 、
、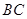 边上的点,满足
边上的点,满足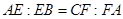
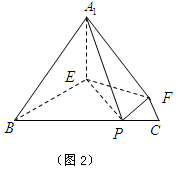
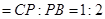 (如图1).将△
(如图1).将△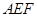 沿
沿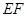 折起到
折起到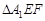 的位置,使二面角
的位置,使二面角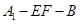 成直二面角,连结
成直二面角,连结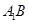 、
、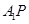 (如图2)
(如图2)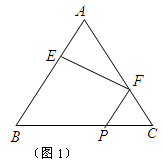
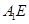 ⊥平面
⊥平面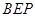 ;
;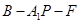 的余弦值.
的余弦值.