Ő‚ńŅńŕ»›
°ĺŐ‚ńŅ°Ņń≥–£łŖ∂Ģ£®1£©įŗ—ß…ķő™Ńň≥ÔīŽĺ≠∑—łÝįŗ…ŌĻļ¬ÚŅőÕ‚∂ŃőÔ£¨įŗőĮĽŠ≥…ŃĘŃň“ĽłŲ…ÁĽŠ Ķľý–°◊ť£¨ĺŲ∂®ņŻ”√ ÓľŔįň‘¬∑›£®30Őžľ∆ň„£©¬÷ŃųĽĽįŗ»•Ōķ Ř“Ľ÷÷ ĪŃÓňģĻŻ.‘ŕ’‚30Őžńŕ√ŅĹÔňģĻŻĶń ’»Ž![]() £®‘™£©”Ž Īľš
£®‘™£©”Ž Īľš![]() £®Őž£©Ķń≤Ņ∑÷ żĺ›»ÁŌ¬ĪŪňý ĺ£¨“—÷™»’Ōķ Ř
£®Őž£©Ķń≤Ņ∑÷ żĺ›»ÁŌ¬ĪŪňý ĺ£¨“—÷™»’Ōķ Ř![]() £®ĹÔ£©”Ž Īľš
£®ĹÔ£©”Ž Īľš![]() £®Őž£©¬ķ◊„“ĽīőļĮ żĻōŌĶ.
£®Őž£©¬ķ◊„“ĽīőļĮ żĻōŌĶ.
£®1£©łýĺ›ŐŠĻ©ĶńÕľŌůļÕĪŪłŮ£¨Ō¬≥Ý√ŅĹÔňģĻŻĶń ’»Ž![]() £®‘™£©”Ž Īľš
£®‘™£©”Ž Īľš![]() £®Őž£©ňý¬ķ◊„ĶńļĮ żĻōŌĶ Ĺľį»’Ōķ ŘŃŅ
£®Őž£©ňý¬ķ◊„ĶńļĮ żĻōŌĶ Ĺľį»’Ōķ ŘŃŅ![]() £®ĹÔ£©”Ž Īľš
£®ĹÔ£©”Ž Īľš![]() £®Őž£©Ķń“ĽīőļĮ żĻōŌĶ£Ľ
£®Őž£©Ķń“ĽīőļĮ żĻōŌĶ£Ľ
£®2£©”√![]() £®‘™£©ĪŪ ĺŌķ ŘňģĻŻĶń»’ ’»Ž£¨–ī≥Ų
£®‘™£©ĪŪ ĺŌķ ŘňģĻŻĶń»’ ’»Ž£¨–ī≥Ų![]() ”Ž
”Ž![]() ĶńļĮ żĻōŌĶ Ĺ£¨≤Ę«ů’‚30Őž÷–ĶŕľłŐž»’ ’»Ž◊Óīů£¨◊Óīů÷Ķő™∂ŗ…Ŕ‘™£Ņ
ĶńļĮ żĻōŌĶ Ĺ£¨≤Ę«ů’‚30Őž÷–ĶŕľłŐž»’ ’»Ž◊Óīů£¨◊Óīů÷Ķő™∂ŗ…Ŕ‘™£Ņ

°ĺīūįł°Ņ£®1£©ľŻĹ‚őŲ£®2£©‘ŕĶŕ ģŐž Ī»’ ’»Ž◊Óīů£¨◊Óīů÷Ķő™90‘™.
°ĺĹ‚őŲ°Ņ ‘Ő‚∑÷őŲ£ļ£®1£©Ņ……Ť![]() £¨”…ŌŖ∂ő
£¨”…ŌŖ∂ő![]() ĻżĶ„
ĻżĶ„![]() £¨
£¨ ![]() Ķ√
Ķ√![]() £ĽĶń÷Ķ£¨”…ŌŖ∂ő
£ĽĶń÷Ķ£¨”…ŌŖ∂ő![]() ĻżĶ„
ĻżĶ„![]() £¨
£¨ ![]() Ķ√
Ķ√![]() Ķń÷Ķ£¨ī”∂ÝŅ…Ķ√ĹŠĻŻ£Ľ£®2£©Ō»«ů≥ŲŌķ ŘňģĻŻĶń»’ ’»ŽĶńļĮ żĻōŌĶ Ĺ
Ķń÷Ķ£¨ī”∂ÝŅ…Ķ√ĹŠĻŻ£Ľ£®2£©Ō»«ů≥ŲŌķ ŘňģĻŻĶń»’ ’»ŽĶńļĮ żĻōŌĶ Ĺ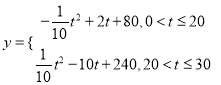 £¨ņŻ”√∂ĢīőļĮ ż∑÷ĪūŇ–∂Ō≥Ų£¨ŃĹ∂őļĮ żĶńĶ•Ķų–‘£¨ņŻ”√Ķ•Ķų–‘∑÷Īū«ů≥Ų◊Óīů÷Ķ£¨‘ŔĪ»ĹŌīů–°ľīŅ….
£¨ņŻ”√∂ĢīőļĮ ż∑÷ĪūŇ–∂Ō≥Ų£¨ŃĹ∂őļĮ żĶńĶ•Ķų–‘£¨ņŻ”√Ķ•Ķų–‘∑÷Īū«ů≥Ų◊Óīů÷Ķ£¨‘ŔĪ»ĹŌīů–°ľīŅ….
‘Ő‚Ĺ‚őŲ£ļ£®1£©“ņŐ‚“‚Ņ……Ť![]() £¨ĶĪ
£¨ĶĪ![]() Ī£¨ŌŖ∂ő
Ī£¨ŌŖ∂ő![]() ĻżĶ„
ĻżĶ„![]() £¨
£¨ ![]() Ķ√
Ķ√![]() £Ľ
£Ľ
ĶĪ![]() Ī£¨ŌŖ∂ő
Ī£¨ŌŖ∂ő![]() ĻżĶ„
ĻżĶ„![]() £¨
£¨ ![]() Ķ√
Ķ√![]() .
.
ňý“‘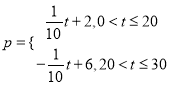 .
.
ŃÓ![]() £¨”…ĪŪ÷– żĺ›Ķ√
£¨”…ĪŪ÷– żĺ›Ķ√![]() £¨ňý“‘
£¨ňý“‘![]() .
.
£®2£©”…![]() Ķ√
Ķ√
ĶĪ![]() Ī£¨
Ī£¨ ![]() ‘ŕ
‘ŕ![]() …ŌĶńĶ•ĶųĶ›‘Ų£¨‘ŕ
…ŌĶńĶ•ĶųĶ›‘Ų£¨‘ŕ![]() …ŌĶ•ĶųĶ›ľű£¨ňý“‘ĶĪ
…ŌĶ•ĶųĶ›ľű£¨ňý“‘ĶĪ![]() Ī£¨
Ī£¨ ![]() ”–◊Óīů÷Ķő™
”–◊Óīů÷Ķő™![]() ‘™£ĽĶĪ
‘™£ĽĶĪ![]() Ī£¨
Ī£¨ ![]() ‘ŕ
‘ŕ![]() …ŌĶ•ĶųĶ›ľű£¨ňý“‘
…ŌĶ•ĶųĶ›ľű£¨ňý“‘![]() .
.
◊ŘļŌ…Ō ŲĶ√£ļ‘ŕĶŕ ģŐž Ī»’ ’»Ž◊Óīů£¨◊Óīů÷Ķő™90‘™.
