题目内容
若a>0,b>0,且函数f(x)=4x3-ax2-2bx-2在x=1处有极值,则ab的最大值为( )
| A.2 | B.3 | C.6 | D.9 |
D
解析

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
定义域为R的函数f(x)满足f(1)=1,且f(x)的导函数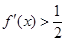 ,则满足
,则满足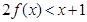 的x的集合为( )
的x的集合为( )
| A.{x|x<1} | B.{x|-1<x<1} | C.{x|x<-1或x>1} | D.{x|x>1} |
设函数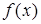 在R上可导,其导函数为
在R上可导,其导函数为 且函数
且函数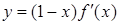 的图像如图所示,则下列结论一定成立的是( )
的图像如图所示,则下列结论一定成立的是( )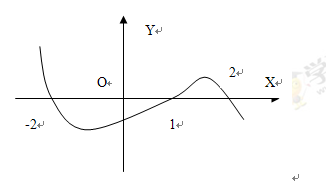
A.函数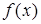 的极大值是 的极大值是 ,极小值是 ,极小值是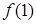 |
B.函数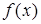 的极大值是 的极大值是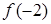 ,极小值是 ,极小值是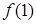 |
C.函数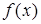 的极大值是 的极大值是 ,极小值是 ,极小值是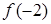 |
D.函数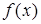 的极大值是 的极大值是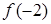 ,极小值是 ,极小值是 |
曲线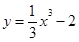 在点
在点 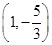 处切线的斜率为( )
处切线的斜率为( )
A. | B. | C. | D. |
若曲线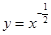 在点
在点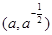 处的切线与两坐标轴围成的三角形面积为18.则
处的切线与两坐标轴围成的三角形面积为18.则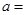 ( )
( )
| A.64 | B.32 | C.16 | D.8 |
定义域为R的函数f(x)满足f(1)=1,且f(x)的导函数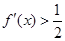 ,则满足
,则满足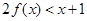 的x的集合为( )
的x的集合为( )
| A.{x|x<1} | B.{x|-1<x<1} | C.{x|x<-1或x>1} | D.{x|x>1} |
函数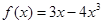 (
( )的最大值是( )
)的最大值是( )
A.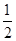 | B.-1 | C.0 | D.1 |
函数f(x)=x2-2ax+a在区间(-∞,1)上有最小值,则函数g(x)=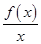 在区间(1,+∞)上一定( )
在区间(1,+∞)上一定( )
| A.有最小值 | B.有最大值 | C.是减函数 | D.是增函数 |
 ,g(x)=xα在点P(1,1)处的切线分别为l1,l2,且l1⊥l2,则实数α的值为( )
,g(x)=xα在点P(1,1)处的切线分别为l1,l2,且l1⊥l2,则实数α的值为( )