题目内容
若曲线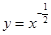 在点
在点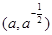 处的切线与两坐标轴围成的三角形面积为18.则
处的切线与两坐标轴围成的三角形面积为18.则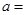 ( )
( )
| A.64 | B.32 | C.16 | D.8 |
A
解析试题分析:求导数可得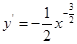 ,所以在点
,所以在点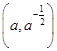 处的切线方程为:
处的切线方程为: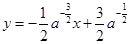 ,
,
令x=0,得y=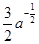 ;令y=0,得x=3a.
;令y=0,得x=3a.
所以切线与两坐标轴围成的三角形的面积 S=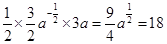 ,解得a=64
,解得a=64
故选A.
考点:导数的几何意义,利用导数研究曲线上某点切线方程.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
函数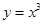 的单调递增区间是( )
的单调递增区间是( )
A.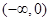 | B. | C.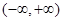 | D.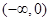 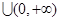 |
已知函数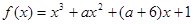 有极大值和极小值,则
有极大值和极小值,则 的取值范围为( )
的取值范围为( )
A.-1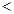  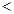 2 2 | B.-3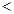  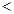 6 6 |
C. 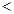 -1或 -1或 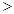 2 2 | D. 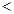 -3或 -3或 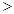 6 6 |
对任意的x∈R,函数f(x)=x3+ax2+7ax不存在
极值点的充要条件是( )
| A.a=0或a="7" | B.a<0或a>21 | C.0≤a≤21 | D.a=0或a=21 |
曲线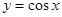
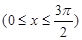 与坐标轴所围成图形面积是( )
与坐标轴所围成图形面积是( )
| A.4 | B.2 | C.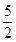 | D.3 |
函数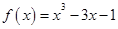 ,若对于区间[-3,2]上的任意x1,x2,都有 | f(x1)-f (x2)|≤ t,则实数t的最小值是( )
,若对于区间[-3,2]上的任意x1,x2,都有 | f(x1)-f (x2)|≤ t,则实数t的最小值是( )
| A.20 | B.18 | C.3 | D.0 |
函数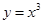 在
在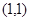 处的切线与
处的切线与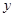 轴交点的纵坐标为( )
轴交点的纵坐标为( )
A. | B. | C.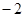 | D. |
若a>0,b>0,且函数f(x)=4x3-ax2-2bx-2在x=1处有极值,则ab的最大值为( )
| A.2 | B.3 | C.6 | D.9 |
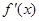 是函数
是函数 的导函数,将
的导函数,将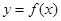 和
和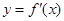 的图象画在同一个直角坐标系中,不可能正确的是( )
的图象画在同一个直角坐标系中,不可能正确的是( )