题目内容
2.在Rt△ABC中,∠C=90°,AC=4,BC=2,D是BC的中点,若E是AB的中点,P是△ABC(包括边界)内任一点.则$\overrightarrow{AD}$•$\overrightarrow{EP}$的取值范围是( )| A. | [-6,6] | B. | [-9,9] | C. | [0,8] | D. | [-2,6] |
分析 首先,分别以CA,CB二直线为x,y轴,建立平面直角坐标系,从而可求出图形上各点的坐标,可设P(x,y),根据条件知P点在△ABC内部及其边界上.这样即可求出$\overrightarrow{AD}•\overrightarrow{EP}=-4x+y+7$,设z=-4x+y+7,从而y=4x+z-7,通过求该直线在y轴上的截距z-7的最大、最小值,便可求出z的最大、最小值,从而得出$\overrightarrow{AD}•\overrightarrow{EP}$的取值范围.
解答 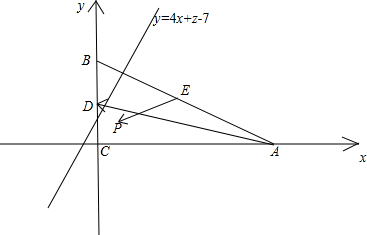 解:如图,以边CA,CB所在直线分别为x,y轴,建立平面直角坐标系,则:
解:如图,以边CA,CB所在直线分别为x,y轴,建立平面直角坐标系,则:
A(4,0),B(0,2),D(0,1),E(2,1);
设P(x,y),P点在△ABC内部包括边界,则:
$\overrightarrow{AD}=(-4,1),\overrightarrow{EP}=(x-2,y-1)$;
∴$\overrightarrow{AD}•\overrightarrow{EP}=-4(x-2)+y-1=-4x+y+7$;
设z=-4x+y+7,则y=4x+z-7,该式表示斜率为4,在y轴上的截距为z-7的直线;
由图形看出当直线y=4x+z-7过点B时,z-7取最大值2,∴z取最大值9;
当该直线过点A时,z-7取最小值-16,∴z取最小值-9;
∴z的范围,即$\overrightarrow{AD}•\overrightarrow{EP}$的范围为[-9,9].
故选:B.
点评 考查建立平面直角坐标系,利用向量坐标解决数量积问题的方法,数量积的坐标运算,以及线性规划的方法求变量的范围.

练习册系列答案
 53随堂测系列答案
53随堂测系列答案
相关题目
12.已知函数f(x)=x2+(a-1)x+4在区间(-∞,4)上是减函数,则实数a的取值范围是( )
| A. | a≤5 | B. | a≥5 | C. | a≤-7 | D. | a≥-7 |
10.等差数列{an}的前n项和为Sn,已知a5=3,S5=10,则a13的值是( )
| A. | 1 | B. | 3 | C. | 5 | D. | 7 |
14.已知|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=1,$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为$\frac{π}{3}$,那么|$\overrightarrow{a}$-4$\overrightarrow{b}$|等于( )
| A. | 2 | B. | 2$\sqrt{3}$ | C. | 6 | D. | 12 |
12.已知函数$f(x)=3sin(2x+\frac{3π}{2})(x∈R)$,下列结论错误的是( )
| A. | 函数 f(x)的最小正周期为π | B. | 函数 f(x)是偶函数 | ||
| C. | 函数 f(x)的图象关于直线$x=\frac{π}{4}$对称 | D. | 函数 f(x)在区间$[0,\frac{π}{2}]$上单调递增 |