已知点P在直线2x+3y-1=0的两侧.且a＞0.b＞0.则$\frac{a-1}{b}$的取值范围是．题目和参考答案——青夏教育精英家教网——

题目内容

13．已知点P（a，b）与点Q（1，0）在直线2x+3y-1=0的两侧，且a＞0，b＞0，则$\frac{a-1}{b}$的取值范围是（-∞，-3）．

分析由题意得到关于a，b的约束条件，画出可行域，然后根据$\frac{a-1}{b}$的几何意义求范围．

解答解：因为点P（a，b）与点Q（1，0）在直线2x+3y-1=0的两侧，所以（2a+3b-1）（2-1）＜0，即2a+3b-1＜0，又a＞0，b＞0，
所以a，b满足的平面区域是，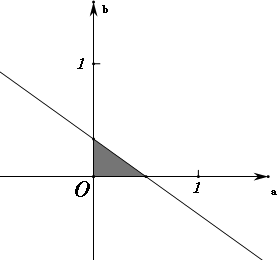
而$\frac{a-1}{b}$表示过（1，0）与区域内的点的直线斜率，所以$\frac{a-1}{b}$＜-3；
故答案为：（-∞，-3）．

点评本题考查了简单线性规划的运用解决代数式的取值范围问题解答的关键是明确a，b的约束条件，正确画图，利用目标函数的几何意义求最值．

练习册系列答案

西城学科专项测试系列答案

小考必做系列答案

小考实战系列答案

小考复习精要系列答案

小考总动员系列答案

小升初必备冲刺48天系列答案

68所名校图书小升初高分夺冠真卷系列答案

伴你成长周周练月月测系列答案

小升初金卷导练系列答案

萌齐小升初强化模拟训练系列答案

相关题目

3．已知二项式（1+$\sqrt{2}$x）ⁿ=a₀+a₁x+a₂x²+…+a_nxⁿ（x∈R，n∈N）
（1）若展开式中第五项的二项式系数是第三项系数的3倍，求n的值；
（2）若n为正偶数时，求证：a₀+a₂+a₄+a₆+…+a_n为奇数．
（3）证明：C${\;}_{n}^{1}$+2C${\;}_{n}^{2}$•2+3C${\;}_{n}^{3}$•2²+…+nC${\;}_{n}^{n}$•2^n-1=n•3^n-1（n∈N⁺）

4．设随机变量X等可能取1、2、3…n值，如果p（X≤4）=0.4，则n值为（　　）

1．函数f（x）=（x²-x+1）e^x（其中e是自然对数的底数）在区间[-2，0]上的最大值是$\frac{3}{e}$．

8．设函数f（x）=x²+4x-1．
（1）若对一切实数x，f（x）+（m-1）x²-（4+m）x＜0恒成立，求m的取值范围；
（2）若对于任意x∈[-1，2]，f（x）＜-m+5恒成立，求m的取值范围．

18．已知集合M={-1，0，1，2}和N={0，1，2，3}的关系的韦恩图如图所示，则阴影部分所示的集合是（　　）

{-1，0，1，2，3}

5．若函数$f（x）=\sqrt{3}sinωx+cosωx$的图象向右平移$\frac{π}{3}$个单位后所的图象关于y轴对称，则ω的值可以是（　　）

2．在Rt△ABC中，∠C=90°，AC=4，BC=2，D是BC的中点，若E是AB的中点，P是△ABC（包括边界）内任一点．则$\overrightarrow{AD}$•$\overrightarrow{EP}$的取值范围是（　　）

3．已知x，y均为正数，θ∈（$\frac{π}{4}$，$\frac{π}{2}$），且满足$\frac{sinθ}{x}$=$\frac{cosθ}{y}$，$\frac{co{s}^{2}θ}{{x}^{2}}$+$\frac{si{n}^{2}θ}{{y}^{2}}$=$\frac{10}{3（{x}^{2}+{y}^{2}）}$，则$\frac{x}{y}$=（　　）

$\frac{\sqrt{3}}{3}$

$\frac{3\sqrt{10}}{10}$