题目内容
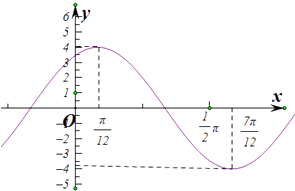
【题目】已知函数f（x）=2cosxsin（x+ 
）﹣a，且x=﹣ 
是方程f（x）=0的一个解．
（1）求实数a的值及函数f（x）的最小正周期；
（2）求函数f（x）的单调递减区间；
（3）若关于x的方程f（x）=b在区间（0， 
）上恰有三个不相等的实数根x1 ， x2 ， x3 ， 直接写出实数b的取值范围及x1+x2+x3的取值范围（不需要给出解题过程）
【答案】
（1）解：函数f（x）=2cosxsin（x+ 
）﹣a，且x=﹣ 
是方程f（x）=0的一个解，
∴f（﹣ ）=0，
即2cos（﹣ ）sin（﹣ + ）﹣a=0，
解得a=sin = 
，
∴f（x）=2cosxsin（x+ ）﹣
=2cosx（ 
sinx+ cosx）﹣
= 
sinxcosx+cos2x﹣
= sin2x+ 
﹣
= sin2x+ cos2x
=sin（2x+ ）；
∴函数f（x）的最小正周期为T= 
=π
（2）解：令 
+2kπ≤2x+ ≤ 
+2kπ，k∈Z，
解得 +kπ≤x≤ 
+kπ，k∈Z；
∴函数f（x）的单调递减区间是[ +kπ， +kπ]，（k∈Z）
（3）解：关于x的方程f（x）=b在区间（0， 
）上恰有三个不相等的实数根x1，x2，x3，
则实数b的取值范围是（ ，1）；
x1+x2+x3的取值范围是（ 
， ）
【解析】（1）根据f（﹣ ）=0求出a的值，再化简f（x），求出f（x）的最小正周期；（2）根据正弦函数的图象与性质，即可求出f（x）的单调递减区间是；（3）根据函数f（x）的图象与性质，结合题意，即可得出b与x1+x2+x3的取值范围．
备战中考寒假系列答案
【题目】（本小题满分12分） 某中学的环保社团参照国家环境标准制定了该校所在区域空气质量指数与空气质量等级对应关系如下表（假设该区域空气质量指数不会超过
）：
空气质量指数 |
|
|
|
|
|
|
空气质量等级 |
|
|
|
|
|
|
该社团将该校区在
年
天的空气质量指数监测数据作为样本，绘制的频率分布直方图如下图，把该直方图所得频率估计为概率．
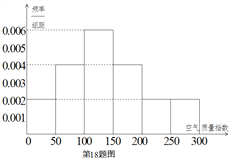
（Ⅰ）请估算
年（以
天计算）全年空气质量优良的天数(未满一天按一天计算)；
（Ⅱ）该校
年
月
、
日将作为高考考场，若这两天中某天出现
级重度污染，需要净化空气费用
元，出现
级严重污染，需要净化空气费用
元，记这两天净化空气总费用为
元，求
的分布列及数学期望．
