题目内容
已知c>0,p:函数y=cx是R上的减函数;q:当x∈[
,2]时,函数f(x)=x+
>c2-
c+3恒成立.若p∧q为假命题且p∨q是真命题,求c的取值范围.
| 1 |
| 2 |
| 1 |
| x |
| 5 |
| 2 |
若p是真命题,则0<c<1;
若命题p是真命题,由x∈[
,2]得,函数f(x)=x+
的值域为[2,
],
∴有c2-
c+3<2⇒
<c<2.
若p∧q为假命题且p∨q是真命题,
则p,q有且只有一个为真.
(1)若p真q假,则
,解得0<c≤
;
(2)若p假q真,则
,解得1≤c<2.
故实数c的取值范围是(0,
]∪[1,2).
若命题p是真命题,由x∈[
| 1 |
| 2 |
| 1 |
| x |
| 5 |
| 2 |
∴有c2-
| 5 |
| 2 |
| 1 |
| 2 |
若p∧q为假命题且p∨q是真命题,
则p,q有且只有一个为真.
(1)若p真q假,则
|
| 1 |
| 2 |
(2)若p假q真,则
|
故实数c的取值范围是(0,
| 1 |
| 2 |

练习册系列答案
相关题目
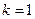 ”是“函数
”是“函数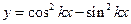 的最小正周期为
的最小正周期为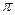 ”的充要条件;
”的充要条件;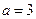 ”是“直线
”是“直线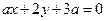 与直线
与直线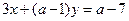 相互垂直”的充要条件;
相互垂直”的充要条件;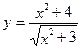 的最小值为
的最小值为
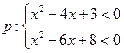 ,则
,则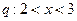 ,那么其逆否命题写成若
,那么其逆否命题写成若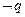 则
则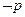 应该是 .
应该是 .