Question

【题目】已知椭圆右焦点是抛物线的焦点，是与在第一象限内的交点，且.

（1）求的方程；

（2）已知菱形的顶点在椭圆上，顶点在直线上，求直线的方程.

Answer 1

【答案】（1）；（2）.

【解析】

试题分析：（1）由抛物线的定义结合求出的坐标，由椭圆的定义可得求得椭圆方程；（2）直线的方程为：，在菱形中，，设直线的方程为，联立直线的方程与椭圆的方程可得.由点、在椭圆上，知，以及、中点在上，由此能导出直线的方程.

试题解析：（1）设，由抛物线定义，，因为，所以，即.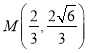

所以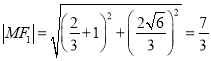，由椭圆定义得：

，

所以，∴椭圆的方程为.

（2）因为直线的方程为，为菱形，所以，设直线的方程为，

代入椭圆的方程为，得，

由题意知，.

设，则，

所以中点坐标为，

由为菱形可知，点在直线上，

所以.

∴直线的方程为，即.