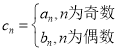题目内容
【题目】设函数![]() ,函数
,函数![]()
![]()
(1)当![]() 时,解关于
时,解关于![]() 的不等式:
的不等式: ![]() ;
;
(2)若![]() 且
且![]() ,已知函数
,已知函数![]() 有两个零点
有两个零点![]() 和
和![]() ,若点
,若点![]() ,
, ![]() ,其中
,其中![]() 是坐标原点,证明:
是坐标原点,证明: ![]() 与
与![]() 不可能垂直。
不可能垂直。
【答案】(1)见解析;(2)见解析.
【解析】试题分析:(1)当![]() 时,原不等式可化为
时,原不等式可化为![]() ,分为
,分为![]() ,
, ![]() ,
, ![]() 和
和![]() 几种情形得结果;(2)由韦达定理可得
几种情形得结果;(2)由韦达定理可得![]() 和
和![]() ,利用反证法得最后结果.
,利用反证法得最后结果.
试题解析:(1)当![]() 时,由
时,由![]() 有
有![]() ,即
,即![]() ,当
,当![]() 时,有
时,有![]() ,解得:
,解得: ![]() 当
当![]() 时,
时, ![]() ,解得:
,解得: ![]() 或
或![]() ,当
,当![]() 时,
时, ![]() ,所以 当
,所以 当![]() 时,
时, ![]() ,解得:
,解得: ![]() 当
当![]() 时,
时, ![]() ,此时无解 当
,此时无解 当![]() 时,
时, ![]() ,解得:
,解得: ![]() ,综上: 当
,综上: 当![]() 时,原不等式的解集为:
时,原不等式的解集为: ![]() ,当
,当![]() 时,原不等式的解集为:
时,原不等式的解集为: ![]() ,当
,当![]() 时,原不等式的解集为:
时,原不等式的解集为: ![]() ,当
,当![]() 时,原不等式的解集为:
时,原不等式的解集为: ![]() ,当
,当![]() 时,原不等式的解集为:
时,原不等式的解集为: ![]() .
.
(2)![]() 时, 由
时, 由![]() 为
为![]() 的两根可得,
的两根可得, ![]() ,
, ![]()
假设![]() ,即
,即![]() ,故
,故![]() ,即
,即![]() ,所以
,所以![]() 从而有
从而有![]() ,即
,即 ![]()
故![]() 即
即![]() ,这与
,这与![]() 矛盾.故
矛盾.故![]() 与
与![]() 不可能垂直.
不可能垂直.

练习册系列答案
相关题目