题目内容
【题目】某工厂加工一批零件，加工过程中会产生次品，根据经验可知，其次品率p与日产量x（万件）之间满足函数关系式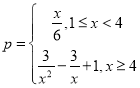
，已知每生产1万件合格品可获利2万元，但生产1万件次品将亏损1万元（次品率=次品数/生产量）
（1）试写出加工这批零件的日盈利额y（万元）与日产量x（万件）的函数；
（2）当日产量为多少时，可获得最大利润？最大利润为多少？
【答案】（1）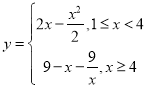
；（2）当日产量为4万元时可获得最大利润
万元.
【解析】
（1）根据合格品可获利2万元，次品将亏损1万元，对
分两种情况讨论，即可得答案；
（2）利用分段函数的性质，求出最大值，即可得答案.
（1）当
时，
当
时，
.
所以函数关系为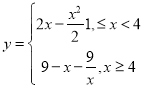
；
（2）当时，
，
所以当
时取得最大值2，
当时，
，
所以在
函数单调递减，所以当
时，y取得最大值，
又
所以当日产量为4万元时可获得最大利润万元.
练习册系列答案
相关题目
