题目内容
9.定义在R上的函数f(x)满足f(x+2)=2f(x),若当0≤x≤2时,f(x)=x(2-x),则当-2≤x≤0时,f(x)=-$\frac{1}{2}$x(x+2).分析 由-2≤x≤0,得0≤x+2≤2,再由题中表达式求得f(x+2),根据f(x+2)=2f(x)从而求得f(x).
解答 解:当-2≤x≤0时,有0≤x+2≤2,
∴f(x+2)=(x+2)[2-(x+2)]=-x(x+2).
又f(x+2)=2f(x),
∴f(x)=$\frac{1}{2}$f(x+2)=-$\frac{1}{2}$x(x+2).
故答案为:-$\frac{1}{2}$x(x+2).
点评 本题考查了求函数解析式的知识,是基础题,其中正确理解函数的概念是解决问题的关键.

练习册系列答案
 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
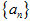 的前
的前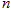 项和为
项和为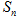 ,已知,
,已知,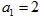 ,且
,且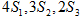 成等差数列.
成等差数列.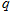 ;
;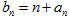 ,求数列
,求数列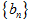 的前
的前 .
.