题目内容
20.设Sn是数列{an}的前n项和,已知a1=4,an+1=Sn+3n,设bn=Sn-3n.(1)证明:数列{bn}是等比数列,并求数列{bn}的通项公式;
(2)令cn=bn+2-2log2bn,求数列{cn}的前n项和Tn.
分析 (1)由an+1=Sn+3n,可得Sn+1-Sn=${S}_{n}+{3}^{n}$,变形${S}_{n+1}-{3}^{n+1}=2({S}_{n}-{3}^{n})$,即bn+1=2bn,即可证明;
(2)cn=2n-1+2-2(n-1)=2n-1-2n.再利用等差数列与等比数列的前n项和公式即可得出.
解答 (1)证明:∵an+1=Sn+3n,∴Sn+1-Sn=${S}_{n}+{3}^{n}$,
化为${S}_{n+1}-{3}^{n+1}=2({S}_{n}-{3}^{n})$,
又bn=Sn-3n.
∴bn+1=2bn,b1=S1-31=1,
∴数列{bn}是等比数列,首项为1,公比为2.
∴bn=2n-1.
(2)解:cn=bn+2-2log2bn=2n-1+2-2(n-1)=2n-1-2n.
∴数列{cn}的前n项和Tn=$\frac{{2}^{n}-1}{2-1}$-2×$\frac{n(n+1)}{2}$
=2n-1-n2-n.
点评 本题考查了等差数列与等比数列的通项公式及其前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.f(x)=cosx-sinx+2sin2x的最大值是( )
| A. | -2-$\sqrt{2}$ | B. | -1 | C. | 2 | D. | $\frac{17}{8}$ |
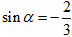 ,且
,且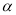 为第四象限角,则
为第四象限角,则 的值等于( )
的值等于( )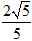 B.
B.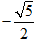 C.
C.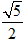 D.
D.