题目内容
10.一支车队有15辆车,某天依次出发执行任务.第1辆车于下午2时出发,第2辆车于下午2时10分出发,第3辆车于下午2时20分出发,依此类推.假设所有的司机都连续开车,并且都在下午6时停下休息.(1)到下午6时,最后一辆车行驶了多长时间?
(2)如果每辆车的行驶速度都是60km/h,这支车队当天一共行驶了多少路程?
分析 (1)根据条件求出时间间隔,即可即可到下午6时,最后一辆车行驶了的时间.
(2)每辆车行驶的时间为:an,则结合等差数列的求和公式进行计算即可.
解答 解:(1)第一辆车出发时间为下午2时,每隔10分钟$\frac{1}{6}$小时出发一辆
则第15辆车在14×$\frac{1}{6}$=$\frac{7}{3}$小时,最后一辆车出发时间为:2+$\frac{7}{3}$=$\frac{13}{3}$小时
第15辆车行驶时间为:6-$\frac{13}{3}$=$\frac{5}{3}$小时(1时40分) …5分
(2)设每辆车行驶的时间为:an,由题意得到{an}是以a1=4为首项,d=-$\frac{1}{6}$为公差的等差数列
则行驶的总时间为:Sn=15×4+$\frac{15×14}{2}$×(-$\frac{1}{6}$)=$\frac{85}{2}$…10分
则行驶的总里程为:S=$\frac{85}{2}$×60=2550(km).
点评 本题主要考查函数的应用问题,利用等差数列的性质是解决本题的关键.

练习册系列答案
相关题目
5.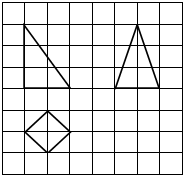 如图,网格纸上小正方形的边长为1,粗实线画出的是某底面为正方形的四棱锥的三视图,则该四棱锥的表面积为( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某底面为正方形的四棱锥的三视图,则该四棱锥的表面积为( )
 如图,网格纸上小正方形的边长为1,粗实线画出的是某底面为正方形的四棱锥的三视图,则该四棱锥的表面积为( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某底面为正方形的四棱锥的三视图,则该四棱锥的表面积为( )| A. | $\sqrt{2}$+$\sqrt{6}$ | B. | 2+2$\sqrt{6}$ | C. | 2+2$\sqrt{2}$+2$\sqrt{6}$ | D. | 2+3$\sqrt{2}$+$\sqrt{22}$ |
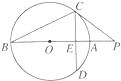 如图,PC切圆O于点C,割线PAB经过圆心O,弦CD⊥AB于点E,若圆O的半径为2,PA=1,求PC•CE的值.
如图,PC切圆O于点C,割线PAB经过圆心O,弦CD⊥AB于点E,若圆O的半径为2,PA=1,求PC•CE的值.