Question

5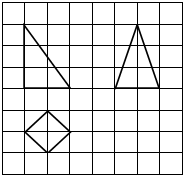．如图，网格纸上小正方形的边长为1，粗实线画出的是某底面为正方形的四棱锥的三视图，则该四棱锥的表面积为（　　）

• A． $\sqrt{2}$+$\sqrt{6}$
• B． 2+2$\sqrt{6}$
• C． 2+2$\sqrt{2}$+2$\sqrt{6}$
• D． 2+3$\sqrt{2}$+$\sqrt{22}$

Answer 1

分析 根据几何体的三视图，得出该几何体是侧棱垂直于底面的四棱锥，且四棱锥的底面为正方形，
结合图中数据求出它的全面积．

解答 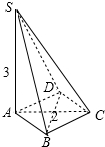解：根据几何体的三视图，得
该几何体是如图所示的四棱锥S-ABCD，且侧棱SA⊥底面ABCD，
底面ABCD是边长为$\sqrt{2}$的正方形；
∴S_△SAB=S_△SAD=$\frac{1}{2}$×3×$\sqrt{2}$=$\frac{3\sqrt{2}}{2}$；S_△SCD=S_△SBC=$\frac{1}{2}$×$\sqrt{2}$×$\sqrt{{3}^{2}{+（\sqrt{2}）}^{2}}$=$\frac{\sqrt{22}}{2}$；
又S_{正方形ABCD}=${（\sqrt{2}）}^{2}$=2，
∴该四棱锥的全面积为S=2+2×$\frac{3\sqrt{2}}{2}$+2×$\frac{\sqrt{22}}{2}$=2+3$\sqrt{2}$+$\sqrt{22}$．
故选：D．

点评 本题考查了空间几何体三视图的应用问题，也考查了求三角形面积的应用问题，是基础题目．