题目内容
1.设抛物线y2=2px(p>0),M(a,0),N(b,0)是x轴正半轴上的两个顶点,过M作斜率为k1的直线与抛物线交于A,B两点,延长AN,BN分别于抛物线交于C,D两点,若直线CD的斜率为k2,则$\frac{{k}_{1}}{{k}_{2}}$=$\frac{b}{a}$.分析 设A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4),代入抛物线方程,运用点差法和斜率公式,设出AB的方程为x=my+a,代入抛物线方程,运用韦达定理,化简整理,即可得到所求值.
解答 解:设A(x1,y1),B(x2,y2),C(x3,y3),D(x4,y4),
则y12=2px1,y22=2px2,
两式相减,可得(y1-y2)(y1+y2)=2p(x1-x2),
即有k1=$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=$\frac{2p}{{y}_{1}+{y}_{2}}$,
同理可得k2=$\frac{2p}{{y}_{3}+{y}_{4}}$,
即有$\frac{{k}_{1}}{{k}_{2}}$=$\frac{{y}_{3}+{y}_{4}}{{y}_{1}+{y}_{2}}$,
设AB的方程为x=my+a,代入抛物线方程可得:
y2-2pmy-2pa=0,
即有y1+y2=2pm,y1y2=-2pa,
由AC和BD与抛物线相交,可得y1y3=-2pb,
y2y4=-2pb,
即有y3=$\frac{-2pb}{{y}_{1}}$,y4=$\frac{-2pb}{{y}_{2}}$,
则$\frac{{k}_{1}}{{k}_{2}}$=$\frac{{y}_{3}+{y}_{4}}{{y}_{1}+{y}_{2}}$=-2pb•$\frac{1}{{y}_{1}{y}_{2}}$=$\frac{b}{a}$.
故答案为:$\frac{b}{a}$.
点评 本题考查直线与抛物线的位置关系,考查韦达定理和直线的斜率公式的运用,考查运算能力,属于中档题.

练习册系列答案
相关题目
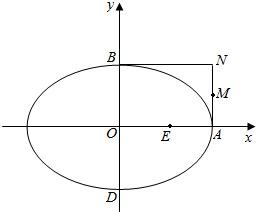 如图所示,椭圆C:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的右顶点是A,上、下两个顶点分别为B、D,四边形OANB是矩形(O为原点),点E、M分别为线段OA、AN的中点.
如图所示,椭圆C:$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的右顶点是A,上、下两个顶点分别为B、D,四边形OANB是矩形(O为原点),点E、M分别为线段OA、AN的中点.