题目内容
甲、乙两个箱子中装有大小相同的小球,甲箱中有2个红球和2个黑球,乙箱中装有2个黑球和3个红球,现从甲箱和乙箱中各取一个小球并且交换。
(1)求交换后甲箱中刚好有两个黑球的概率。
(2)设交换后甲箱中黑球的个数为 ,求
,求 的分布列和数学期望。
的分布列和数学期望。
(1)求交换后甲箱中刚好有两个黑球的概率。
(2)设交换后甲箱中黑球的个数为
 ,求
,求 的分布列和数学期望。
的分布列和数学期望。(1)0.5;(2)1.9.
本试题主要考核了古典概型概率的运用。以及分布列和期望值的求解运算 。
解:(1)甲乙两盒各取一个球交换后,甲盒中恰有2个黑球有下面几种情况:
出的两个球都是黑球,则甲盒恰好有2个黑球的事件记为A1,则P(A1)= …(3分)
…(3分)
②取出的两个球都是红球,则此时甲盒中恰有2个黑球的事件记为A2,则P(A2)=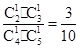 …(6分)
…(6分)
故P1=P(A1)+P(A2)="1" /2 …(8分)
(2)则ξ的分布列为:
ξ 1 2 3
P 3/ 10 1 /2 1/ 5
根据表格,可得ξ的数学期望为Eξ="3/" 10 ×1+1 /2 ×2+1/ 5 ×3="19" /10 …(12分)
解:(1)甲乙两盒各取一个球交换后,甲盒中恰有2个黑球有下面几种情况:
出的两个球都是黑球,则甲盒恰好有2个黑球的事件记为A1,则P(A1)=
 …(3分)
…(3分)②取出的两个球都是红球,则此时甲盒中恰有2个黑球的事件记为A2,则P(A2)=
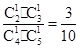 …(6分)
…(6分)故P1=P(A1)+P(A2)="1" /2 …(8分)
(2)则ξ的分布列为:
ξ 1 2 3
P 3/ 10 1 /2 1/ 5
根据表格,可得ξ的数学期望为Eξ="3/" 10 ×1+1 /2 ×2+1/ 5 ×3="19" /10 …(12分)

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
 :“取出的2件产品中至多有1件是二等品”的概率
:“取出的2件产品中至多有1件是二等品”的概率 .
.  ;
; :“取出的2件产品中至少有一件二等品”的概率
:“取出的2件产品中至少有一件二等品”的概率 .
.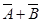 是必然事件
是必然事件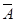 与
与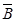 互斥 D、
互斥 D、