题目内容
19.设函数fn(x)=xn(1-x)2在x∈[-$\frac{1}{2}$,1]上最大值为an(n=1,2,3…),求数列{an}的通项公式.分析 利用导数研究函数fn(x)的单调性,对n分类讨论即可得出.
解答 解:${f}_{n}^{′}(x)$=nxn-1(x-1)2+2xn(x-1)=xn-1(x-1)[(n+2)x-n]
=(n+2)xn-1(x-1)$(x-\frac{n}{n+2})$,
列出表格如下:
| x | $[-\frac{1}{2},0)$ | 0 | $(0,\frac{n}{n+2})$ | $\frac{n}{n+2}$ | $(\frac{n}{n+2},1)$ |
| ${f}_{n}^{′}(x)$ | - | 0 | + | 0 | - |
| fn(x) | 单调递减 | 极小值 | 单调递增 | 极大值 | 单调递减 |
${f}_{n}(\frac{n}{n+2})$=$(\frac{n}{n+2})^{n}(\frac{2}{n+2})^{2}$,
∴an=$\left\{\begin{array}{l}{\frac{4{n}^{n}}{(n+2)^{n}},n为奇数}\\{\frac{9}{{2}^{n+2}},n为偶数}\end{array}\right.$.
点评 本题考查了利用导数研究函数的单调性、数列的通项公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
14.“a=-1”是“过点P(2,1)有且只有一条直线与圆R:x2+y2+2ax+ay+2a2+a-1=0相切”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分又不必要条件 |
4.已知甲、乙两名同学高三一年10次数学测试成绩的茎叶图如图所示,则下列说法正确的是( )
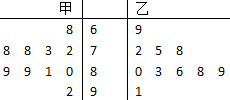

| A. | 甲同学的平均成绩高于乙同学的平均成绩 | |
| B. | 甲同学成绩的中位数大于乙同学成绩的中位数 | |
| C. | 甲同学的成绩要比乙同学的成绩稳定 | |
| D. | 乙同学的成绩要比甲同学的成绩稳定 |