题目内容
8．化简求值：$\frac{1}{co{s}^{2}\frac{A}{2}•cosA}$•$\frac{co{t}^{2}\frac{A}{2}-co{t}^{2}\frac{3A}{2}}{1+co{t}^{2}\frac{3A}{2}}$．分析 利用同角三角函数基本关系式、倍角公式即可得出．
解答 解：∵$\frac{co{t}^{2}\frac{A}{2}-co{t}^{2}\frac{3A}{2}}{1+co{t}^{2}\frac{3A}{2}}$=$\frac{\frac{co{s}^{2}\frac{A}{2}}{si{n}^{2}\frac{A}{2}}-\frac{co{s}^{2}\frac{3A}{2}}{si{n}^{2}\frac{3A}{2}}}{1+\frac{co{s}^{2}\frac{3A}{2}}{si{n}^{2}\frac{3A}{2}}}$=$\frac{co{s}^{2}\frac{A}{2}si{n}^{2}\frac{3A}{2}-si{n}^{2}\frac{A}{2}co{s}^{2}\frac{3A}{2}}{si{n}^{2}\frac{A}{2}}$=$\frac{sin（\frac{A}{2}+\frac{3A}{2}）sin（\frac{3A}{2}-\frac{A}{2}）}{si{n}^{2}\frac{A}{2}}$=$\frac{sin2AsinA}{si{n}^{2}\frac{A}{2}}$．
∴原式=$\frac{1}{co{s}^{2}\frac{A}{2}•cosA}$•$\frac{2si{n}^{2}AcosA}{si{n}^{2}\frac{A}{2}}$
=$\frac{2si{n}^{2}A}{\frac{1}{4}si{n}^{2}A}$=8．
点评 本题考查了同角三角函数基本关系式、倍角公式，考查了计算能力，属于中档题．
练习册系列答案
阅读快车系列答案
相关题目
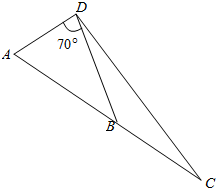为保障行车安全，有关方面决定自2015年3月14日起，对开通至今已27年延安东路隧道进行封闭大修．如图所示，A点是延安东路隧道浦东入口处，B点是人民隧道入口处，C点是复兴东路隧道入口处，A、B、C三点可近似看成在一条直线上．已知AB间距离约为1.2km，BC间距离约为0.8km．现在有一车辆在银城浦东南路路口的D点处此路口到A点的距离约为0.8km，此处连接A点与B点的线段张角为70°．请问这个路口到复兴东路隧道入口的距离约为多少千米？（结果精确到0.1km）